小学两位数乘两位数速算系列题(小学两位数乘两位数速算系列方法)

导语：小学两位数乘两位数速算系列

解构神奇的印度乘法速算

（之三）

今天给大家带来的是印度乘法速算中计算最为简单的特殊模式之一的：“十位相同，个位互补的两位数乘两位数”的算理解构。

“十位相同，个位互补的两个两位数”，就是这两个数的十位都是同一个数字，而它们的个位相加刚好等于“10”，这样的一组两位数还是比较常见的，比如“93×97”，“34×36”，以及个位为“5”的两位数的完全平方，如“652”。符合这种模式的两位数乘法，稍加训练，所有人都可以达到每秒做几题的速度。

由于两个乘数的十位相同，而个位相加等于“10”，所以我们可以将这两个两位数分别表示为“a×10+b”和“(a+1)×10-b”，即第二个数用第一个数凑整以后再减去它的个位（例如：53×57时，可以把57表示为“50+7”，或把53表示为“60-7”）：

与前面的文档一样，我们用代数的方法将它们相乘如下：

观察这个结论式：

“×100”表示的就是百位上的数值，

“×1”表示的就是个位上的数值，因此我们发现这个结论只需要在百位和个位填上数值，

“a×(a+1)”，就是十位乘以它自己加“1”，

“b×(10-b)”，正好就是这两个数的个位相乘；

由于它们的个位相乘只能是两位数，所以甚至连进位都不用考虑，我们就得到了下面的结论：

两个乘数的个位相乘得到积的个位和十位（不足“10”的十位补“0”）；

十位乘以自己加“1”得到积的百位和千位；

用图形表示如下：

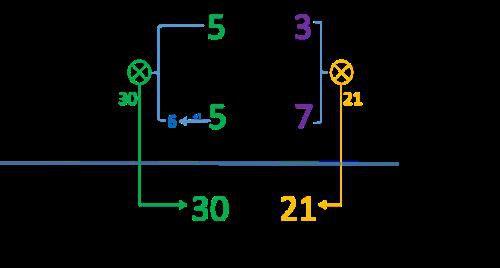
整个计算过程，只需要进行一次加“1”的简单加法和两次乘法就可以完成，全程没有进位，“秒出答案”又一次从理想变为现实。

这就是数学的神奇之处，这种神奇，在数学的奇遇中层出不穷，从计算到几何，从求解方程到看似复杂的问题，一旦你看透了它的本质，就可以“秒出答案”。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小茜创作整理编辑！