导语：数学记忆方法实战，少刷题！教孩子这样学，省力又扎实

数学上涉及的公式，从数量上来讲并不多。但是，数学公式从特征上来讲，比较接近于数字。我们都知道，记忆材料分为图像、声音、文字、数字四大类，大脑对数字的记忆最困难，速度也最慢，并且容易忘记。

如果记忆方法不当，随着学习的深入，对知识的记忆会越来越混乱，学习难度越来越大。比如三角函数，公式很多，变来变去，如果从字面上来记忆，容易把人搞得晕头转向。

数学知识，更要强调彻底理解，找到规律。

一个简单的例子

全等三角形，是初中就开始学习的知识，但是高中的几何包括立体几何都是经常要用到的。如果不熟悉，很多高中几何题都没法做。

理科知识就是有这样的特点，都是一环扣一环的，前面学不好，后面学起来就会很难，回过头再来补，要耗费更多的时间和精力。

全等三角形的定义

经过翻转、平移后，能够完全重合的两个三角形叫做全等三角形。两个三角形全等，说明它们所有的边和所有对应的角都相等。

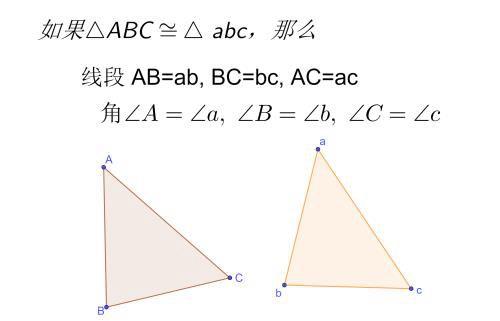
判定定理（要记忆的内容）

判定两个三角形是否全等，也就是如何根据已有条件判定两个三角形是否全等，即是否符合性质“对应边相等，对应角相等”。

（边边边）SSS（Side-Side-Side）：三边对应相等的三角形是全等三角形。（边角边）SAS（Side-Angle-Side）：两边及其夹角对应相等的三角形是全等三角形。 （角边角）ASA（Angle-Side-Angle）：两角及其夹边对应相等的三角形全等。 （角角边）AAS（Angle-Angle-Side）：两角及其一角的对边对应相等的三角形全等。（直角、斜边、直角边）RHS（Right angle-Hypotenuse-Side）（又称HL定理【斜边、 直角边】）：在一对直角三角形中，斜边及另一条直角边相等。

下列两种方法不能验证为全等三角形：

（角角角）AAA（Angle-Angle-Angle）：三角相等，不能证全等，但能证相似三角形。 （边边角）SSA（Side-Side-Angle）：其中一角相等，且非夹角的两边相等。 

用途

判定定理通常用来证明两个三角形全等，依据全等三角形的性质，可以得出“对应的边和角相等”。在证明几何题的时候，经常要用它来证明一些线段相等或者角相等。

方法不对，刷题白费

全等三角形的判定定理虽然只有这么几条，但是死记硬背的话也很容易混淆。

很多孩子上课的时候听得稀里糊涂，课后也不及时总结，在学习这块知识的时候，会直接记忆口诀，比如：“边边边、边角边、角边角、角角边、直斜边”。这种方式短期内看起来很快，但是时间长了就容易记混，根本不知道说的是什么意思，在应用的时候也容易出错。

如果不彻底理解，那么即使大量刷题，对知识的记忆仍然不够深刻，甚至还会有漏洞。这样情况下大量刷题，准确率是会随之提高，但这很可能只是个假象，是“知其然，而不知其所以然”，只是记住了题型而不是知识，题型一变化就容易出错。

而且刷题得到的是短期和中期记忆，过了一个学期记忆效果就大打折扣了。以后再用到这块知识的时候，连简单的口诀都记不清，至于怎么应用，就更搞不清楚了。这样基础不牢，会给后面的学习带来很大的障碍。

刷题再多，如果只是为了短期提分，而没有增进理解，那么花再多的功夫也是白白浪费了。

理清脉络，彻底理解，找到规律，做题少也能记得牢

人类的大脑记忆符号的能力不怎么样，可是它也很神奇，对规律的记忆十分牢固。即便是复杂的规律，只要能够理解，知道来龙去脉，能够和已有的知识体系或者直觉体验相融合，就能恒久不忘。

要想找到规律，前面的功课要做足。不用急于刷题，而是花些时间理解和总结。学得好的孩子，通常不是刷题最多的孩子，而是把这一步做深做透的孩子。

彻底理解，理清脉络，找到规律，对应到学习方法上，就是课后复习和总结的环节。课上在老师讲解下理解，并不代表就真的理解了。在课后尝试自己推导整个过程，整理成自己的知识体系下能够理解的形式，才是真的彻底理解。

这个过程其实真正做起来，还是比较简单和容易操作的，比较熟练和养成习惯的孩子，课后几分钟就能完成。没有养成习惯的孩子，前期要花费一定的时间，逐步适应，直到熟练和养成习惯。

下面我们以全等三角形判定定理的理解为例，介绍这个过程。

一、从头开始

两个三角形，有三条对应边，和三个对应角，一共有六个要素。至少要有三个要素对应相等才能判定全等。那么这三个要素对应相等有多少组合呢？

第一种组合：三条边相等第二种组合：三个角相等第三种组合：两个角，一条边第四种组合：两条边，一个角

二、推导过程

1.三条边相等

三角形是稳定的，三条边相等，它是不会变形的。所以三条边对应相等的两个三角形肯定全等。

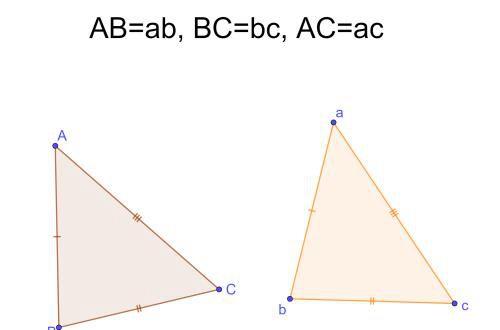
2.三个角相等

三个角相等的情况下，只能判定这两个三角形相似。但是边的长短可能不一样，一个大一个小。

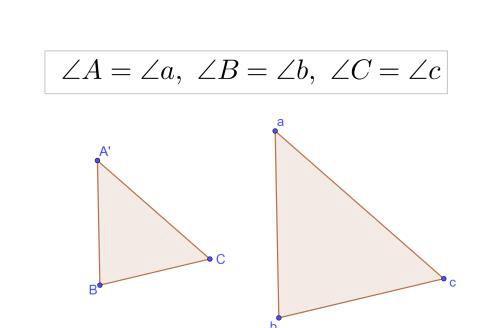
3.两个角，一条边

三角形内角和是180°，已知两个角对应相等，那么剩下那个角一定也相等，那么这两个三角形至少是相似的。再加上一条边，大小就固定了。这里分两种情况：

一种情况是对应边相等，两个三角形肯定是全等的；

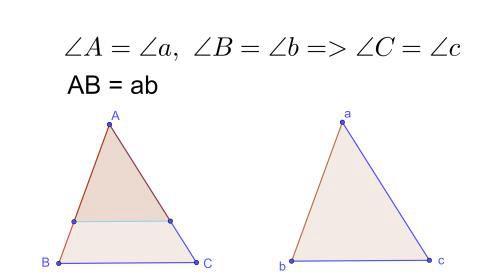
另一种情况是两条边不是对应边，那么这两个三角形不一定全等。

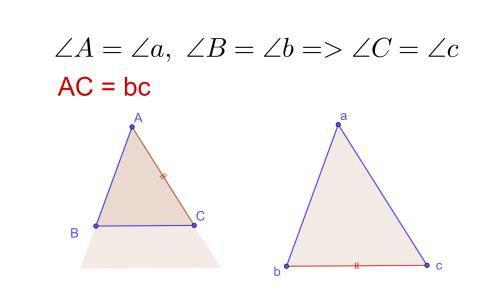
4.两条边，一个角

这个是比较容易搞混的地方。

如果两条边相等，夹角相等，那么两个三角形全等；

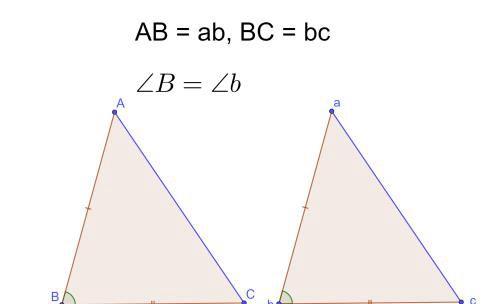
如果两条边相等，相等的不是夹角，那么两个三角形不一定全等；

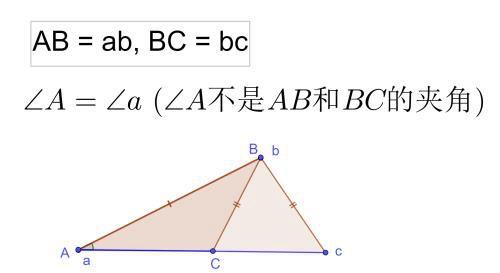
特殊情况，当相等的对应角不是夹角，但它是个直角的时候，两个三角形也全等。因为直角三角的三条边有这样的性质，a²+b²=c²。知道斜边和一条直角边相等，则第三条直角边一定相等。

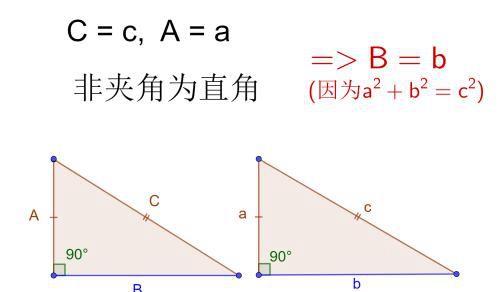
三、整理成思维导图

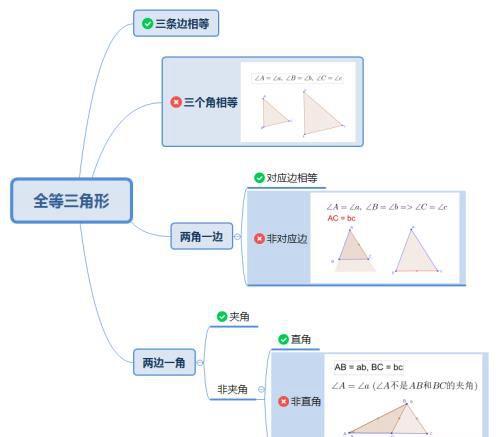
当孩子能够根据自己的理解整理成这样的思维导图，对于全等三角形这块知识，就记忆得很清楚、很牢固了。

直接背诵边边边、边角边之类的口诀，好像能够一分钟就能记下来，但是很快就忘了怎么回事，做题的时候不知道什么情况下能用，什么情况不能用。这样的记忆速度快，但是总体效率低，效果并不好。

彻底理解，找到规律，理清脉络，再记忆的这种方式，看起来不是什么捷径，但是记起来清楚明白，而且很牢固。不仅记住了角边角，而且记住了它在什么情况下能用，什么情况下不能用。而且更重要的是，你很清楚地知道为什么能用，或者为什么不能用。

彻底理解，找到规律，理清脉络，才能激活大脑的潜能，这样记公式，绝对不用担心会记错，也不用担心会用错。这样的记忆方式，才是真正最有效率、最有效果的学习方式。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑！