八仙过海(八仙过海口诀)

导语：八仙过海话消元

学完二元一次方程组解法后，老师给出了如下一道题目对大家说：解二元一次方程组的基本思想是消元，而消元的方法常用的有代入消元法和加减消元法两种，下面一题就请同学们八仙过海，各显神通，只要你能消元，不论采用什么样的方法和手段都可以．

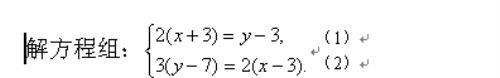
题目一出，张明同学眼明手快，一眼发现方程（1）中y的系数为1，于是抢着发言："可以用代入法消元．

由（1），得y＝2x＋9，　（3）

把（3）代入（2），消去y，得

3（2x＋9－7）＝2（x－3），

解之，得x＝－3，

把x=-3代入（3），得y＝3．”

师：这样消元好！好在能发现y的系数为1，为代入法消元提供了良好的条件．

汉中看了张明的解法后说："张明的消元虽然很容易，但消元后的一元一次方程较复杂，我建议先把方程组化简为：

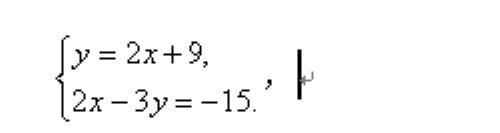
然后再采用代入法消元．"

师：汉中同学说得对，把方程组化简是我们解方程组的优良传统，这个传统值得继承和发扬．

曹睿听了汉中的意见后接着说："干脆把原方程组化为我们平时常见的标准形式：

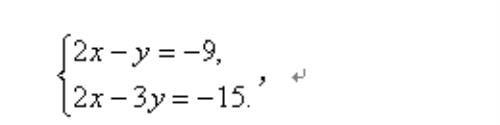
至此不是很容易发现可以用加减法消元吗？"

师：曹睿同学的意见不错，他不仅继承了优良的传统，而且还加以了光大，终于发现了可用人见人爱的加减法进行消元。

韩湘听后说："若用加减法消元，直接把两个方程相加不是也可以消元吗？大家请看：

（1）＋（2），得

2(x＋3)＋3（y－7）=y－3＋2（x－3），

化简，得2y＝6，y＝3．"

师：好厉害的眼光啊！能发现两方程直接相加可以消元的确不容易．可见，先观察，后动笔在解题中是多么的重要啊！

一直沉默的何荷突然发言："把方程组变形为：

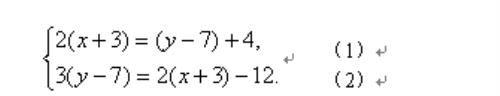
至此，不论是采用代入法，还是采用加减法不都是很容易消元吗？请看：

把（1）代入（2），得

3(y－7)=(y－7)+4－12，

解之，得y＝3．

或（1）＋（2），得

2(y－7)=－8，解得y＝3．"

师：漂亮！何荷同学能够抓住题目的特征，从整体思想出发，把方程组构造为分别以（x＋3）和（y－7）为整体的新方程组，为消元创造良好的环境和条件，实在是件值得喜庆的事．象这种消元法称为整体消元法．其他同学还有不同的解法吗？

"有！"回答的是吕宾，他说："由方程（2），我们可以设

3（y－7）＝2（x－3）＝6k，

则y－7＝2k，x－3＝3k，

从而x＝3k+3，y＝2k+7，

代入方程（1），解得k＝－2，

故x＝－3，y＝3．"

师：妙！吕宾同学利用方程的等积关系，巧妙地采用参数法，通过引入参数k，三下五除二就把x、y给消掉了，求出k后，再求x、y简直就是易如反掌．一般地，若有一个方程是比例形式的就可以采用这种参数法．

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小嫣创作整理编辑！