导语：初中数学，一元一次不等式组应用题，2道例题讲解，配3道练习

一元一次不等式组的应用题，2道例题讲解，配3道练习

一元一次不等式组的应用题：设未知数很关键

例题精选:

例1．把若干个橘子分给几个小朋友，若每个小朋友分3个，则多余8个；每个小朋友分5个，则最后的一名小朋友分得的数不足5个，但是比1个又多，问一共有多少名小朋友？多少个橘子？

分析：

1、每个小朋友分3个橘子，存在倍数关系，所以设小朋友人数设小朋友为x，则橘子有（3x+8）。

2、每个小朋友分5个橘子，按理应该有5x个橘子，可是最后一个分不到5个，说明比原有的橘子数量多了，所以：5x-（3x+8）>0;

5x-（3x+8）=1，说明最后的人能分到4个

5x-（3x+8）=2就能分到3个

5x-（3x+8）=3就能分到2个

5x-（3x+8）=4.就能分到1个

因为最后一个人分到的比1个多，所以5x-（3x+8）<4

解题过程：

解、设小朋友为x，则橘子有（3x+8），得

5x-（3x+8）>0

5x-（3x+8）<4

解得：4<x<6

因为x为整数，所以x=5，5X3+8=23

答：一共有5个小朋友，23个橘子。

例2.某地为灾区进行募捐，共收到粮食100吨，副食品54吨. 现计划租用甲、乙两种货车共8辆将这批货物全部运往灾区，已知一辆甲种货车同时可装粮食20吨、副食品6吨，一辆乙种货车同时可装粮食8吨、副食品8吨。

(1) 将这些货物一次性运到目的地，有几种租用货车的方案？

(2) 若甲种货车每辆付运输费1300元，乙种货车每辆付运输费1000元，要使运输总费用最少，应选择哪种方案？

分析（1）：

1、甲车数+乙车数=8，可设甲车数为x，乙车数为y得，x+y=8，

或者设甲车数为x，则乙车数为（8-x）。

2、甲车运输的粮食+乙车运输的粮食必须大于或等于100吨，副食品必须大于或等于54吨，否则无法完成运输任务。

3、甲车每辆运粮食20吨，x辆可运20x，乙车每辆运粮食8吨，（8-x）辆运粮8（8-x）得出

20x+8（8-x）>=100,同理可得：6x+8（8-x）>=54

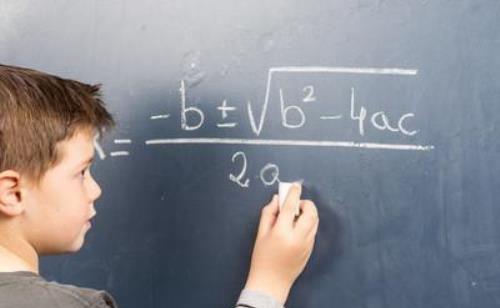
解题过程：

解、设甲车数为x，则乙车数为（8-x）得

20x+8（8-x）>=100

6x+8（8-x）>=54

解得：3<=x<=5,因为x表示车辆为整数，所以x只能是3，4，5,所以有3种方案。

答：有3种租用货车的方案。

分析（2）：

甲车有x辆，每辆1300元，一共是1300x元，

乙车有（8-x）辆，每辆1000元，一共是1000（8-x）元

解题过程：

总费用=1300x+1000（8-x）=300x+8000

因为x越小，300x+8000就越小，

以上三种方案中x最小是3

所以费用最少方案为：甲车3辆，乙车5辆。

小试牛刀

1.某中学为八年级寄宿学生安排宿舍，如果每间4人，那么有20人无法安排，如果每间8人，那么有一间不空也不满，求宿舍间数和寄宿学生人数。

2. 某工程队要招聘甲、乙两种工种的工人150人，甲、乙两种工种的工人月工资分别为600元和1000元.现要求乙种工种的人数不少于甲种工种人数的2倍,问甲、乙两种工种各招聘多少人时，可使得每月所付的工资最少？

3．某厂有甲种原料470㎏,乙种原料420㎏,计划用这两种原料生产A、B两种产品共100件。已知生产一件A种产品需甲种原料6㎏，可获利600元；生产一件B种产品需甲种原料4㎏，乙种原料5㎏，可获利800元。

（1）按题目要求和所给的条件安排A、B两种产品的生产件数，共有几种方案？

（2）在（1）中哪种方案获利最大？最大利润是多少？

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小心创作整理编辑！