三项相乘怎么拆(七彩木喜欢酸性水吗)

导语：一题二套三相乘四分组，因式分解最强十字口诀！转给初中的娃

初中阶段的因式分解的重要性对于刚上初中的孩子来说不言而喻，然而很多老师都课堂上花了时间讲解，但尴尬的是孩子总是做的不好，那问题到底是出在孩子身上？还是老师没有教好？个人觉得不管原因出在哪，咱们更多的是放在知识点本身，接下来吴老师带你们一起探究一下如何理解初中阶段因式分解的十字口诀！

俗话说的好，工欲善其事必先利其器。首先咱们回顾一下因式分解的定义：把一个多项式化为几个最简整式的乘积的形式，这种变形叫做把这个因式分解（也叫作分解因式）。拆解一下一定要注意两点：一定是乘积的形式；一定是最简形式。因式分解是我们初中阶段解决许多数学问题的有力工具，比如后面的一元二次方程求解，二次函数等等。由于因式分解方法灵活，技巧性强，学习这些方法与技巧，不仅是掌握因式分解内容所必需的，而且对于培养学生的解题技能，发展学生的思维能力，都有着十分独特的作用。

首先我们来捋一下解题的思路，拿到一题因式分解的题目第一反应是问问自己有没有公因式可以提取，如果有公因式想都不用想先提取公因式，如果没有再进行下一步。

接下来带各位复习下提公因式法：

一般地，如果多项式的各项有公因式，可以把这个公因式提到括号外面，将多项式写成因式乘积的形式，这种分解因式的方法叫做提公因式法.。

例如：am+bm+cm=m(a+b+c)

顺道送你们一句口诀：找准公因式，一次要提净；全家都搬走，留1把家守；提负要变号，变形看奇偶。

光说不练假把式，光练不说傻把式。接下来我们来一道真题练练手。

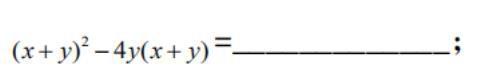
这道题拿到手很多初学者一般不会按照之前讲过的思路走，第一步竟然不是考虑有公因式（x+y）可以提取，而是先想着去括号，然后再做文章。这样虽然最后也能分解出来，但这样就有点缘木求鱼了。所以最简单的做法就是先提取公因式（x+y），然后结果一下就出来了。

所以告诉孩子拿到题目先问自己能不能提？不能就进行下一步，接着再问问自己能不能套用公式？能套用公式咱们就套用公式，那套用公式无非就逆用平方差和完全平方公式，极少数情况下会利用到下面第三个立方的公式。

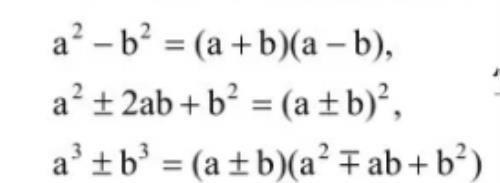
下面两道经典的题目大家练习下，注意整体思想的应用。

当题目一提二套都发现进行不了的时候，这时候十字相乘法该出现了。也就是发现因式分解有三项还不能提取公因式或者套用公式的时候，再考虑十字相乘法。

这里要注意很多老师在七年级的时候都不会重点讲解十字相乘法，而是说留到后面的一元二次方程解法的时候讲解。但是我认为因式分解在七年级上册就给同学们讲通透一点比较好，不然模模糊糊的学生理解可能会出现偏差，到时候一元二次方程也不会熟练应用十字相乘法解题。注意上面给的例题是二次项系数为1的，相对来说比较简单，课堂上适当练习二次项不为1 的题目。

以上的三种方法基本上可以应付中考的所有因式分解，因为据老师分析近十年来安徽中考数学分解因式还没有出现过四项或者四项以上的题目，考纲上也不做要求。所以一题二套三相乘是一定要掌握的方法，但是触类旁通，大家一定要对自己提出更多的要求，所以当万一碰到了四项或者四项以上的要你分解因式，大家也不要懵逼，最多就是分组分解因式就可以解决。

分组分解法：把各项合适分组，然后各组之间进行因式分解，再最后在各组之间进行。

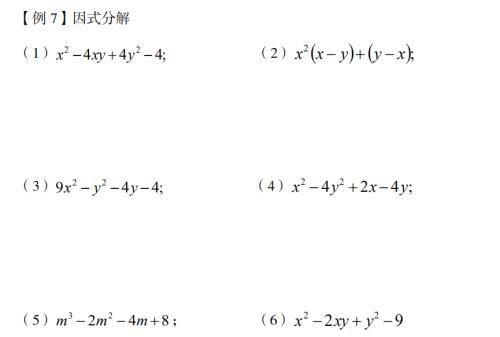
那么问题来了分组到底如何分？其实很简单，比如让你给一个班级分两组，那你打算怎么分？那有人可能就会说我按性别分组，有的人可能会说按照成绩分组，那不管怎么分组，都会有一个标准的，所以因式分解也一样，你为什么这样分组，你要有依据，而依据就是前面总结的分的小组内部能提取公因式，套用公式或者十字相乘。但是注意并不是分组了就一定能做出来，这个还需要大量练习。不信我们来看！

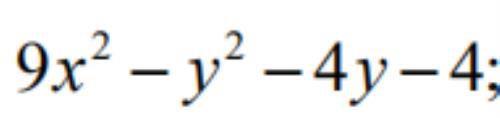
比如这一道题，很多同学会首先可以把1，4项放一组，2，3项放一组，分组一居室1，4项能用平方差公式，2，3项能提取Y,但是这种2+2分组最后会进行不下去，所以应该考虑3+1分组，把2，3，4项分一组，可以用完全平方公式，然后继续用平方差公式分解。所以并不是说你知道了分组就一定能第一次就分对，还需要做题积累哦！

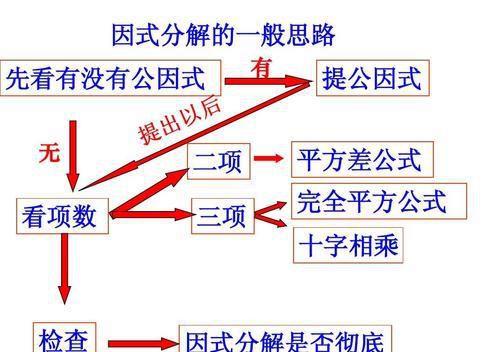
最后再次总结一下因式分解十字口诀，一提二套三相乘四分组，祝愿各位初中因式分解笑傲江湖！

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小竹创作整理编辑！