二次函数怎样判断abc的符号(怎样判断二次函数的abc)

导语：如何判断二次函数中a、b、c的符号，看完就懂

二次函数图象的说法：

二次函数y＝ax²＋bx＋c的图像是一个抛物线，所以也可以说“抛物线y＝ax²＋bx＋c”，这两种说法没什么不同，你喜欢哪种就用哪种。

接下来说说如何判断二次函数表达式中的常数“a、b、c”的符号。

如何判断a的符号：

a大于0时，抛物线开口向上，反之也成立；a小于0时，抛物线开口向下，反之也成立。所以a的符号通常是根据抛物线的开口方向确定的。

如何判断b的符号：

b存在于抛物线的对称轴x＝－b/2a中，所以一般根据对称轴的符号来判断b的符号。

例如：已知抛物线开口向上，对称轴在x轴的左侧，判断b的符号：

抛物线开口向上，则a＞0；对称轴在x轴左侧，则－b/2a＜0；很容易得出b＞0。

如何判断c的符号：

对于二次函数y＝ax²＋bx＋c，当x＝0时，y＝c，所以抛物线与y轴的交点坐标是(0,c)，由此可以得出如下结论：c＞0时，抛物线与y轴正半轴相交，反之也成立；c＜0时，抛物线与y轴负半轴相交，反之也成立。所以，c的符号通常是根据抛物线与y轴正、负半轴的相交情况确定。

根据前面的分析，现在咱们大致了解了a、b、c三个字母的符号的判断方法：根据抛物线开口方向判断a的符号；根据对称轴的符号来判断b的符号；根据抛物线与y轴哪个半轴相交来判断c的符号。

接下来讲解如何判断a、b、c组合出来的代数式的符号。

如何判断a＋b＋c的符号：

对于二次函数y＝ax²＋bx＋c，当x＝1时，函数值y＝a＋b＋c，所以只需判断x＝1时的函数值的符号，就是a＋b＋c的符号。

同理，只需判断x＝－1时的符号，就是a－b＋c的符号；只需判断x＝2时的符号，就是4a＋2b＋c的符号；等等。

不知道你听懂了没有？没太懂也没关系，结合下面这2道例题，你就能做到清清楚楚，明明白白。

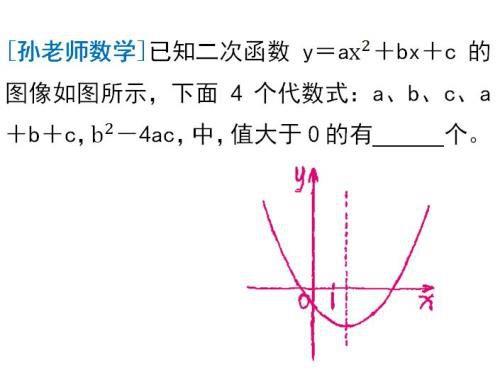
例1

请结合上面所讲，弄明白下面的解析过程。

例如，判断a＋b＋c的详细过程：根据题中的示意图可知，当x＝1时，二次函数的图像在x轴下方，即对应的函数值为负数，把x＝1代入二次函数的表达式y＝ax²＋bx＋c中可得函数值y＝a＋b＋c，所以a＋b＋c是负数。

例2

先通过确定a、b、c的符号，判断①和②的对错，过程如下。

判断③4a＋2b＋c＞0的对错：

如下图，根据抛物线的对称性可知：BM＝AM＜1，所以OB＝1＋BM＜2，所以2在点B的右侧，所以当x＝2时，函数值y是负数，把x＝2代入y＝ax²＋bx＋c得函数值y＝4a＋2b＋c，所以4a＋2b＋c＜0；故③错。

判断④的对错：

如上图，当x＝1时，函数值y＞0，即a＋b＋c＞0；当x＝－1时，函数值y＜0，即a－b＋c＜0；所以：

加油！

本文内容由小悦整理编辑！