两类曲线积分和两类曲面积分(两类曲线积分的区别与联系)

导语：两类曲线积分和曲面积分如何理解掌握

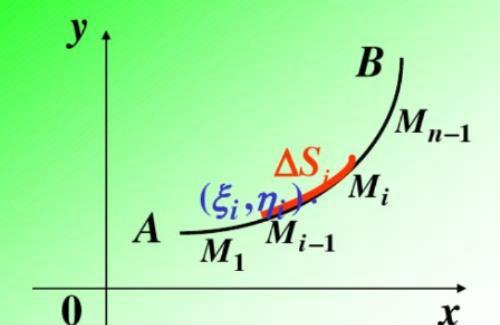
首先是对弧长的曲线积分：

对弧长的曲线积分道理很简单，就是求一条线密度会变化f（x,y）的弧长的质量。

对弧长的曲线积分只要把ds怎么求搞清楚了就行。上式是对一个坐标轴进行投影。

对坐标的曲线积分则是求变力沿曲线所作的功。由于力有方向，并且曲线也有方向，所以对坐标的曲线积分是两个向量，即力与有向线段的点积。P、Q是变力在两个坐标轴的分量。

上式是对两个个坐标轴进行投影。上图中右端积分可以分开逐项计算。

由以上几个图很容易搞清楚对坐标的曲线积分的原理。

对面积的曲面积分就是求面密度变化的一块曲面的质量。

曲面积分最重要的地方在于要把一个曲面的切平面的法向量搞清楚。

上图是面积元素ds在xoy平面通过切平面的法向量投影公式。

从以上分析看到，对坐标的曲面积分其实就是将流体的速度，一个三维空间向量，与曲面的切平面的法向量作点积运算。

向量的点积运算如上图。

对坐标的曲面积分公式如上。公式的左端同样可以分开计算。

与对面积的曲面积分不同，对坐标的曲面积分必须对三个平面，即xoy,yoz,xoz都进行投影，然后计算求和。这是由流体速度的空间属性决定的。

以上是z=f(x,y)的空间曲面切平面法向量的推导过程。

简单总结：

1：对弧长的曲线积分是为了求出线密度变化的弧长质量，是对一个坐标轴进行投影运算。2：对坐标的曲线积分是为了求出变力沿有向弧段所做的功，所以两者必须进行点积运算，且必须对两个坐标轴进行投影运算求和，这是由变力是矢量的特点决定的。

3：对面积的曲面积分是为了求出面密度变化的空间曲面的质量，只要对一个坐标平面，比如xoy平面进行投影运算即可。

4：对坐标的曲面积分是为了求出具有空间速度矢量的流体流出有向曲面的流量，因此也必须两者做点积运算，同时必须在三个坐标平面进行投影运算，然后求和。

5：理解平面曲线的切向量和空间曲面切平面的法向量，是掌握以上知识的关键。

本文内容由小涵整理编辑！