全导数和偏导数的转换公式(全导数和偏导数的转换方法)

导语：全导数和偏导数的转换

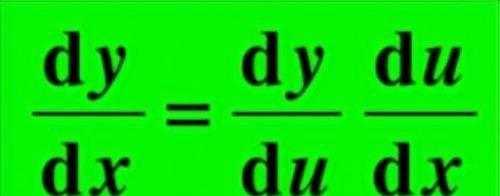
一元复合函数求导法则：

当扩展为二元复合函数以后：

推广：

上述结果就是全导数。注意全导数的中间变量可以是多个，但最终变量只有一个t。

如果有多个最终变量，则称为偏导数：

以上都有两个最终变量x和y，所以得出的结果是偏导数。

先看第一种特殊情况：

图1

上图特殊在于，x,y都既是中间变量，又是最终变量。

上图要特别注意的是 z 的偏导数与 f 偏导数的区别。z 的偏导数是把 z 看作是最终变量 x,y 的函数，而 f 是看作是中间变量u,x,y的函数，两者虽然形式上相等，但观察的角度是不一样的。前者是最终变量，后者是中间变量，因为

的后面其实还要乘上一个

再看下面这种情况：

上图的中间变量都只有同一个最终变量 x，因此问题就转变成了全导数问题。

上图中，

下面看一个例子：

这里

现在要求出 z 对 x 的二阶偏导数。

一阶直接套公式：

图2

二阶按一阶的商求导数也没问题：

图3

那如何到下一步的：

图4

这里关键是

等于什么？假设F(x,y,z)=(x^2)yz-1=0，那么Fx=2xyz，还是x,y,z的函数，而z又是x,y的函数，所以上式就必须通过图1的方式对 Fx 求偏导，利用图2，得到

图3中另一项Fz对x求偏导也一样处理，所以得到图4 的结果。其中

综上：

1：全导数和偏导数的区别就在于最终变量的个数，前者一个，后者多个。当偏导数的最终变量只有一个的时候，就转变成了全导数。

2：注意形如z=f(u,v,x)方程中 z 和函数 f 在意义上的区别。

本文内容由小茜整理编辑！