线性规划可行域的定义是什么(线性规划问题存在可行域则可行域一定包含坐标原点)

导语：高中数学线性规划可行域含参求解参数值的方法

例 若

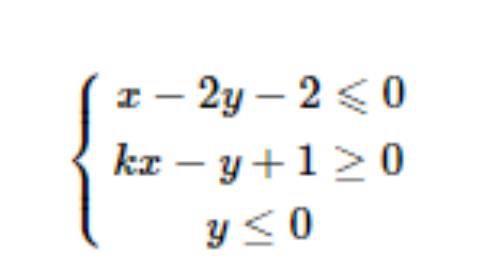
满足约束条件，z=3x+2y的最小值为-18，求k的值。

解：不能画出可行域？没事，我们可以画出一部分来

由z=3x+2y的最小值为-18，得直线：3x+2y=-18经过可行域。

分析：kx-y+1≥0，可知原点在该不等式表示的平面内，且直线kx-y+1=0过点（0,1），当k变化时，直线kx-y+1=0绕点（0,1）转动。对k进行讨论：

（1）当k=0时，由kx-y+1≥0，得y≤1，则可行域区域如图所示：

由z=3x+2y，得y=-3/2x+z/2，可知，截距最小时，z取得最小值。作直线y=-3/2x，向左平移时，截距变小，由于可行域左边不封闭，目标函数无最小值，与已知条件矛盾。

（2）当k>0时，kx-y+1=0得y=kx+1，则会出现以下几种情况：

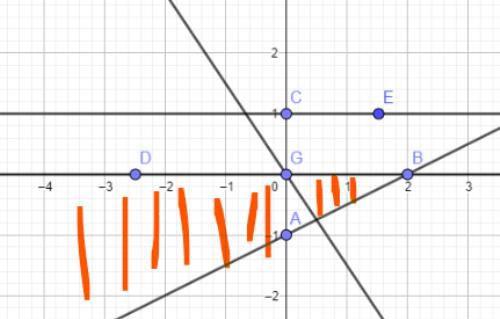
a, 0＜k≤1/2时，如图所示：

由于可行域左边不封闭，目标函数无最小值，与已知条件矛盾。

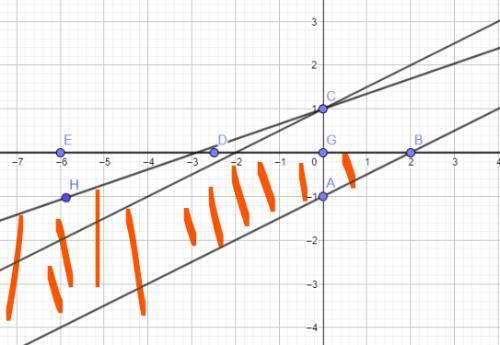
b，当k＞1/2且y=kx+1与直线3x+2y=-18的交点位于G和H中间的E点时，如图所示：

结合图像很容易看到直线3x+2y=-18不是目标函数的直线，与已知条件矛盾。

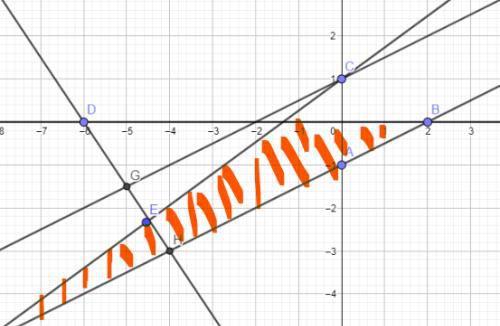
c, 当y=kx+1与直线3x+2y=-18相交时，如图所示：

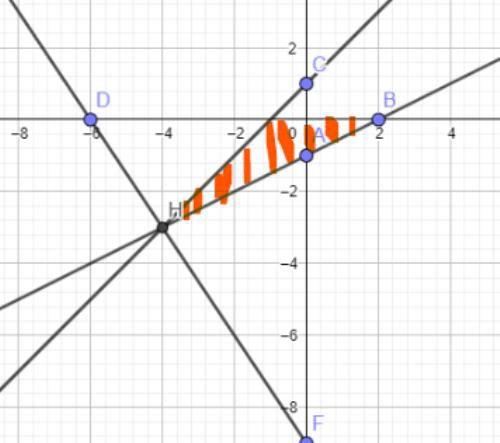
易知直线3x+2y=-18为目标函数的直线，符合题意，解方程组得交点坐标为（-4，-3），带入直线y=kx+1得k=1

d, 当k＞1时，如图所示：

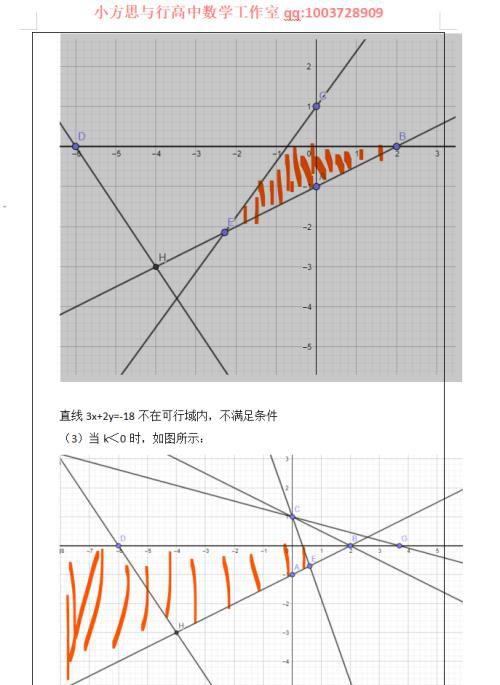
可行域左边不封闭，所以目标函数无最小值。

综上所述：k=1

总结：

解决可行域含参数且已在目标函数的最值求解参数的取值的问题，基本步骤还是线性规划数形结合五部曲的方法，只是，其中需要对参数的取值范围进行讨论，然后结合图像就可以得出参数的取值，重要的是含参数的直线方程经过定点，这是解决此类问题的一个关键点。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！