矩阵的秩的几何意义(矩阵的秩意味着什么)

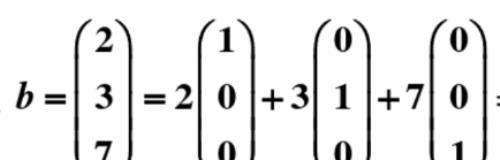
导语：矩阵的秩有什么几何意义

关于矩阵的基，最简单的解释就是：

上图的三个列向量就分别相当于三维空间中的三个坐标轴：

这里转发一篇讨论这个问题的论文：

就是证明贝塔向量组中的r个向量是n个向量组的一个基。

上图中的推导，是因为中间的等式左边每一项都分别含有a1,a2,......an，然后将它们分别按照a1,a2,.....an进行重新组合，从而得到下面那个等式，继而利用阿尔法向量组的无关假设。

这一步很简单，其实就是r个方程有r+1个未知数，所以一定有非零解。（2）就相当于直接把（1）中的h用x代替，方程个数相等但增加了一个变量。

上述定理的证明过程，也可以按照下述方法：

两种方法加以对比，可以加深对这个问题的理解。

关于矩阵的秩，还有如下定理：

矩阵的转置不改变矩阵的秩，就是因为Er是对称的。

由以上推导过程可以看出，如果把n维向量看作一个集合，那么，这个集合中的每一个向量都可以由它的基来表示，就像任何一个三维向量，都可以看作是三维坐标系中的一个点，而这个点在由三根坐标轴构成的坐标系中都有它的坐标一样。因此，n维向量的基的个数r就可以看作是用于表示这个n维向量的坐标系的坐标轴的根数，也就是r根。这个结论对于向量的行和列都是一样的。

本文内容由小鸣整理编辑！