构造垂心证明两线垂直4例怎么写(如何证明垂心taa×oa)

导语：构造垂心证明两线垂直4例

三角形的三条高交于一点，该点叫做三角形的垂心。我们可以利用这一特点构造出三角形两边上高的交点，另一边上的高一定经过该点，从而证明两条线段相垂直。

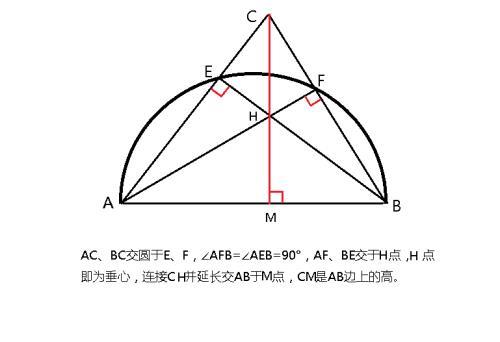
题目1：如图三角形ABC，AB是圆O的直径，如何用无刻度尺作出AB边上的高。

解题思路：根据直径所对的圆周角是直角，连接AF、BE可知∠AFB∠AEB=90°。AF和BE交点H为△ABC的垂心，连接CH并延长交AB于M点，CM必是AB边上的高。

题目2：如图1所示：在四边形ABCD中，△ABD是正三角形，∠BCD=120°，BC=CD，点E，F分别在 BC, CD边上。∠EAF=30°，AE、 AF 分别交BD于M、N点， 连接EN， FM交于G，求证AG ⊥EF。

解题思路：在△AEF中，顶点E、F分别与对边N、M相连，交点为G，如能证明该点为垂心，则结论可成立。

已知△BCD为等腰三角形，∠BCD=120°，故∠CBD=∠BDC=30°，∠ABE=∠ADF=90°。在四边形ABEN中，∠EBN=∠EAN=30°，A、B、E、N四点共圆，∠ABE=∠ANE=90°，EN⊥AF。

同理可证明FM⊥AE。

G点为△AEF的垂心，连接AG并延长交EF必垂直之。

题目3：如图所示，在三角形ABC中，AB

=BC，D为AC的中点，DE与BC垂直于E，F为DE的中点，AE与BF交于G;求证：AE与BF垂直。

解题思路：三角形ABC为等腰三角形，D点为AC中点，连接BD，则BD⊥AC。过F点作MN∥AC交BD于M，交BC于N， MN⊥BD。

在△EDC中，F为DE的中点，则N为EC的中点。

在△AEC中，D为AC的中点，连接DN，则DN∥AE。

在△BDN中，DE⊥BN， MN⊥BD，两垂线的交点F为垂心，BF延长线垂直于DN，即垂直于AE。

题目4：在矩形ABCD中，P在BC上方，AM⊥CP于M，DN⊥BP于N，AM与DN延长线交于K，证明PK⊥BC。

解题思路：采取平移法将BN、CM两条相交的垂线平移为AE、DF两条相交的垂线。

过P点作PH，使PH平行且等于AB或CD，这样就构成了两个平行四边形ABPH和PHDC，延长PH交AD于L，则PL⊥AD和BC。

在△KAD中，连接AH并延长交KD于E，则AE⊥KD；同样DF⊥KA，点H为△KAD的垂心，则KH⊥AD和BC。

根据定理“过一点有且只有一条直线与已知直线垂直”， PH⊥AD和BC，同样KH⊥AD和BC，两条垂线均经过H点，故K、P、H共线，PK⊥BC和AD。

本文内容由快快网络小德整理编辑！