高考立体几何大题详解及答案(高考立体几何大题详解答案)

导语：高考立体几何大题详解

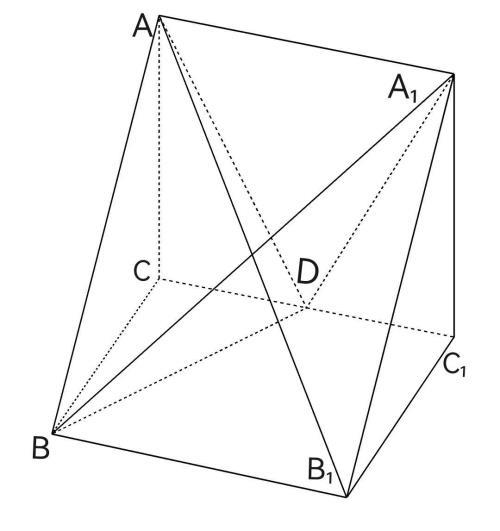
如图1，正三棱柱ABC-A₁B₁C₁的所有棱长都为2，D为CC₁的中点.

（1）求证：AB₁⊥平面A₁BD.

（2）求锐二面角A-A₁D-B的余弦值.

图1

解题分析第一问:线面垂直证明

在证明线面垂直问题时，一般有两种方法供我们选择:几何法、相量法。

几何法

几何法证明线面垂直时，可用定理及推论有四种。

1）证明直线和平面内的两条相交直线垂直；

2）证明和直线平行的另外一条直线垂直于平面；

3）证明直线垂直于平面的另一个平行平面；

4）证明直线所在平面与待证明平面垂直，且该直线垂直于交线；

针对该问题，很显然只有方法1）适用，详细解题步骤见第二小节。

相量法

建立空间直角坐标系后，求出平面的法向量，通过向量计算求出待证明直线和法向量的角度为0，应用到几何法的定理推论2），可知直线与平面垂直。

几何法+向量法

建立直角坐标系，求出直线向量、平面内两条相交直线的向量，计算直线和两条相交直线的各自夹角，可得出直线垂直于平面内的两条相交直线，从而得出直线垂直于平面。

该题中三种方法作者都进行了尝试，第三种方法（几何法+向量法）更为简单快捷、直接明了，所以推荐使用该方法求值。

第二问:面面夹角求值

在进行二面角求值时，也可以分为几何法和向量法两种方法，但是几何法需要做多条辅助线，相比较而言向量法更为直接。

几何法

首先选择其中一个平面中的一点，向两个平面交线做垂线，例如本题中可以选择A点向A₁D做垂线AM；再选择另外一个平面中的一点，向交线做垂线，本题中即为点B，垂线为BN。不难看出两条垂线AM和BN不相交与一点，则需要做出BN过M点的平行线，相交A₁B于点P，则∠AMP即为二面角，通过已知条件计算出余弦值即可。

如下就是做出辅助线之后的图形，笔者并未标注点名称，屏幕前的你能否挑战一下呢？

二面角求解图

向量法

向量法则要简单的很多，求出两个平面的法向量，利用公式cos〈n₁，n₂〉即可求得结果。

综合几何法和向量法，笔者在这里推荐，立体几何的大题，尽量用向量法求解，不仅可以节省时间，还能节省脑力，这一点在高考中尤为重要。如果时间充裕，可以选择几何法来进行验证。

素质养成

该题基本符合高考立体几何大题的难度标准，难度属于中档偏上，异面的线线夹角、线面夹角和面面夹角，是高考的必考内容，同学们必须要将解题方法牢记于心，并勤加练习才能高效拿分。且对立体图形的认识，是以后理科生的学习中必不可少的一部分，尤其在物理、化学、高分子等领域，都有着广泛的应用，所以在此时打好基础尤为重要。

PS:该题的详细解题步骤在下一篇文章中给出，记得来对答案哦！

本文内容由快快网络小凡整理编辑！