求四边形面积的题型(求4边形的面积)

导语：一道高中平面几何题-求四边形面积

一道高中平面几何题-求四边形面积

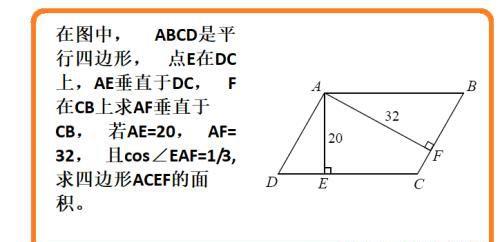
在图中， ABCD是平行四边形， 点E在DC上，AE垂直于DC， F在CB上求AF垂直于CB， 若AE=20， AF=32， 且cos∠EAF=1/3, 求四边形ACEF的面积。

解法1： 如图延长AF与DC的延长线交于点G，

根据已知cosθ=1/3, 所以AG=20/cosθ=60,

这样FG=60-32=28，

但tanθ=2√2, 所以CF=FG/tanθ=28/(2√2)=7√2

同样BF=AF/tanθ=32/(2√2)=8√2

因为sinθ=2√2/3

AB=AF/sinθ=32/(2√2/3)=24√2

EG=AExtanθ=20x2√2=40x√2

由于三角形ABF相似于三角形GCF有相似比BF/CF=8√2/(7√2)=8/7

所以CG=ABx7/8=24√2x7/8=21√2

直角三角形CFG的面积S1=CFxGF/2=7√2x28/2=98√2

直角三角形AEG的面积为S2=AExEG/2=20x40√2/2=400√2

因此四边形ACEF的面积为

S=S2-S1=400√2-98√2=302√2

解法2：如图，

类似上面的解法可以求出AB=24√2， 则可以求出平行四边形ABD的面积为

S1=24√2x20=480√2

同理按照解法可以求出BF=8√2

DE=AE/tanθ=5√2

因而三角形ABF的面积为S2=AFxBF/2=32x(8√2)/2=128√2

三角形AED的面积为S3=AExDE=20x(5√2)/2=50√2

因此四边形AECF的面积为S=S1-S2-S3=302√2

本文内容由小馨整理编辑！