两个三角形边长比例关系(两个三角形边长比例相同叫什么)

导语：一道高中三角题-求三角形的两个边长之比

一道高中三角题-求三角形的两个边长之比

在一个三角形ABC 中， tanA=3/4, tanB=21/20, 求边长AC/BC之比。

解：用三种方法

方法1：利用一条辅助线

如图，做过简图， 并做CD垂直于AB，

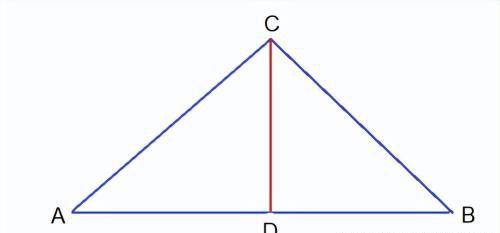
因为AC=CD/sin A

AC=CD/sin B

因此：

AC/BC=sinB/sinA

由于tanA=3/4, 可以看出是3-4-5的直角三角形，所以

Sin A=3/5

同样由于tan B=21/20, 则有相应的直角三角形20-21-29与其对应，

因而sin B=21/29,

最后 AC/BC=sinB/sinA=(21/29)/(3/5)=35/29

方法2：利用正弦定理，

AC/BC=sinB/sin A,

由于tanA=3/4, 那么sinA=3/5

另外tanB=21/20, 所以sinB=21/29

因此

AC/BC=sinB/sin A=（21/29）/(3/5)=35/29

方法3：利用面积的表达式

因为三角形的面积公式可以表达成S=(absinC)/2, 其中a和b是夹角C的两个边长。

分别用角A和角B套用这个公式：

AC·AB·sinA=BC·AB·sinB

得出AC/BC=sinB/sin A,

后面相同。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑！