费马数分解情况(费马定理怎么解的)

导语：费马法分解因数

将一个合数分解成素数相乘，是数论基本问题。

我们凡人的思路是，从2,3,5,7,11……开始一一试，如果能整除则可以将合数分解，如果判断到开方数还没有整除，则这个整数本身就是一个素数。

如分解10379

10379≡1(mod 2)

10379≡2(mod 3)

10379≡4(mod 5)

10379≡5(mod 7)

10379≡6(mod 11)

……

10379≡0(mod 97)

所以，10379被97整除，有一个因数是97

所以，10379=97×107

97和107都是素数，分解完成。

凡人解法优在简单易理解。

我们看看高人费马是如何分解的。

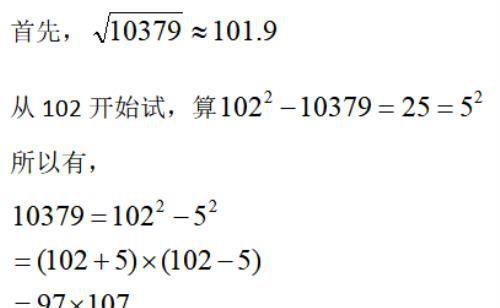
搞定！帅死人

其基本思路是，

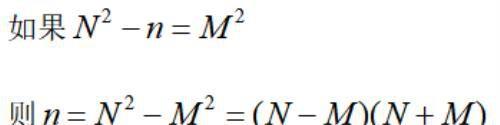
等等，这样算出来，你怎么保证分解完成了，如果97还能继续分解呢？

要判断97是不是素数，只要试2,3,5,7这几个素数就够了，很显然，这几个数都不能整除97，所以，97是素数，不能再分解

对于107，也只要试2,3,5,7就够了，显然它也是素数。

所以，10379=97×107

我们再算一个数93343

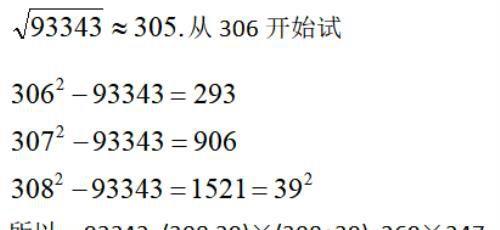
再看269，只要用前几个素数除即可

269≡1(mod 2)

269≡2(mod 3)

269≡4(mod 5)

269≡3(mod 7)

269≡5(mod 11)

269≡9(mod 13)

所以，269是素数

再看347，也只要用前几个素数试试即可

347≡1(mod 2)

347≡2(mod 3)

347≡2(mod 5)

347≡4(mod 7)

347≡6(mod 11)

347≡9(mod 13)

347≡7(mod 17)

所以347是素数

所以，93343=269×347

再看一个更大的数：2027651281

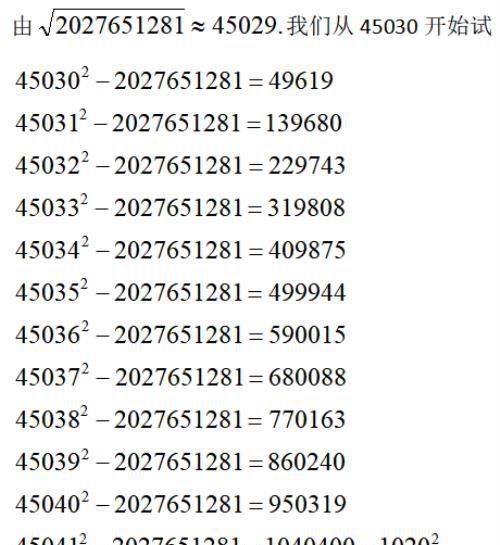
所以，2027651281=(45041-1020)(45041+1020)=46061×44021

我们发现，凡人的思路是从小往中间试，费马的思路是从中间往小试。

于是对于两个因子接近的大数分解，费马法有优势，而两个因子相差很大，凡人的思路还快点。如果待分解的数很大很大，我们并不知道它的因子差是大还是小，蛮难选择的。

所以，费马法分解因数，也就玩玩吧。实用价值不大。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小媛创作整理编辑！