数学集合在高考中的考点(高考数学集合的解题方法)

导语：组合教育：高考数学必考知识点之集合

高考数学集合考试内容：­­

集合、子集、补集、交集、并集．

逻辑联结词．四种命题．充分条件和必要条件．

高考数学考试要求：

（1）理解集合、子集、补集、交集、并集的概念；了解空集和全集的意义；了解属于、包含、相等关系的意义；掌握有关的术语和符号，并会用它们正确表示一些简单的集合．

（2）理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系；掌握充分条件、必要条件及充要条件的意义．

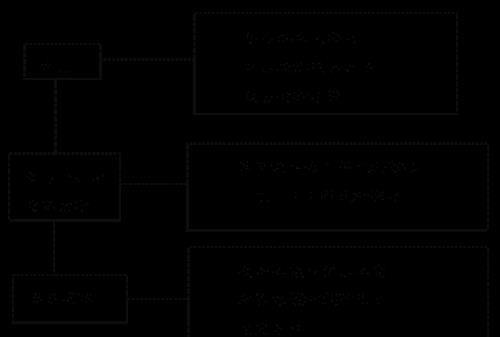
§01. 集合与简易逻辑 知识要点

一、高考数学集合的知识结构:

本章知识主要分为集合、简单不等式的解法（集合化简）、简易逻辑三部分：

二、高考数学集合知识回顾：

（一） 高考数学集合

1. 基本概念：集合、元素；有限集、无限集；空集、全集；符号的使用.

2. 集合的表示法：列举法、描述法、图形表示法.

集合元素的特征：确定性、互异性、无序性.

集合的性质：

4、四种命题的形式：

原命题：若P则q； 逆命题：若q则p；

否命题：若┑P则┑q；逆否命题：若┑q则┑p。

(1)交换原命题的条件和结论，所得的命题是逆命题；

(2)同时否定原命题的条件和结论，所得的命题是否命题；

(3)交换原命题的条件和结论，并且同时否定，所得的命题是逆否命题．

5、四种命题之间的相互关系：

一个命题的真假与其他三个命题的真假有如下三条关系：(原命题

逆否命题)

①、原命题为真，它的逆命题不一定为真。

②、原命题为真，它的否命题不一定为真。

③、原命题为真，它的逆否命题一定为真。

7、反证法：从命题结论的反面出发（假设），引出(与已知、公理、定理…)矛盾，从而否定假设证明原命题成立，这样的证明方法叫做反证法。

本文内容由小涵整理编辑！