向量的混合积的几何意义是什么(向量混合积的几何意义理解)

导语：向量的混合积的几何意义

在讨论向量的混合积之前先回忆一下向量的数量积和向量积。

一、两向量的数量积

我们对向量a和b进行的这样一种运算，运算结果是一个数，它等于|a|、|b|及它们的夹角θ的余弦的乘积。我们把它叫做向量a与b的数量积(或内积)，记作a・b，即

a・b=|a| |b| cosθ。

二、两向量的向量积

如果向量f由两个向量a与b按下述方式定出：f的模|f| =|a| |b| sinθ，其中θ为a、b间的夹角；f的方向垂直于a与b所决定的平面(即f即垂直于a，又垂直于b)，f的指向按右手规则从a转向b来确定，即当右手的四指从a以不超过180度的转角转向b时，竖起的大拇指指向是f的方向。向量f叫做向量a与b的向量积(或外积)，记作a×b，即f=a×b。事实上，a×b的模在数值上等于以向量a和b为边所作平行四边形的面积。

三、向量的混合积

已知三个向量a、b和c，先作两向量a和b的向量积a×b，把所得到的向量与第三个向量c再作数量积(a×b)・c，这样得到的数量叫做三向量a、b、c的混合积，记作[a b c]。

四、向量的混合积的几何意义

向量的混合积[a b c]=(a×b)・c是这样的一个数，它的绝对值等于以向量a、b、c为棱的平行六面体的体积。如果向量a、b、c组成右手系(即c的指向按右手规则从a转向b来确定)，那么混合积的符合是正的，如图1所示；如果a、b、c组成左手系(即c的指向按左手规则从a转向b来确定)，那么混合积的符合是负的。

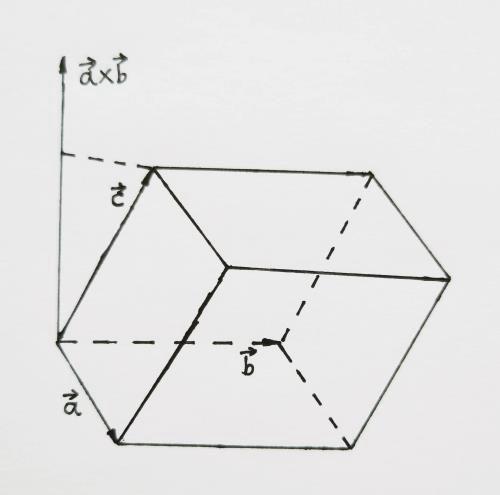
图1

若混合积[a b c]≠0，能以a、b、c三向量为棱构成平行六面体，从而a、b、c三向量不共面；反之，若a、b、c三向量不共面，则必能以a、b、c为棱构成平行六面体，从而[a b c]≠0。三向量a、b、c共面的充分必要条件是他们的混合积 [a b c]=0。

以上内容均为个人理解，如有错误，欢迎指正。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小畅创作整理编辑！