多角度解决问题教学设计(多角度的)
导语:多角度多解法(10种)看一道经典竞赛题
一道经典的题目,其解法也一定是经典的,或者说是有典型性的,并且一定是一题多解的。
下面我们就一起来看一下这道重庆市竞赛题:
【题目】
【如图,在△ABC中,∠C=90°,∠CAD=30°,AC=BC=AD.求证:CD=BD.(重庆市竞赛题)】
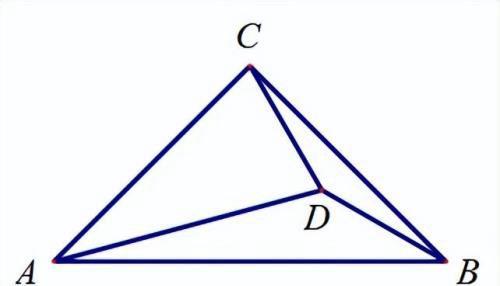
【分析】
这里的30°角给我们以启示,令我们容易想到含30°角的直角三角形、等边三角形等特殊知识;
由AC=BC=AD,使我们容易想到,通过做辅助线让AC、AD与BC产生联系,才能充分利用这些条件;
我们从以下几个方面考虑解这道题:
构造等边三角形;
轴对称(翻折);
其他思路,角平分线等。
【类一】构造等边三角形
以CD为边向两边构造等边三角形;
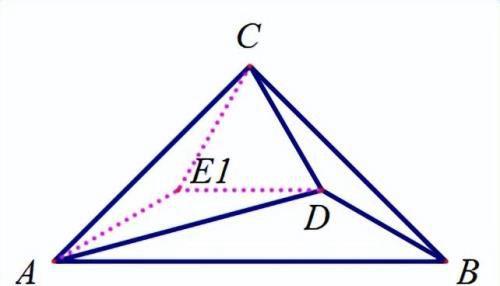
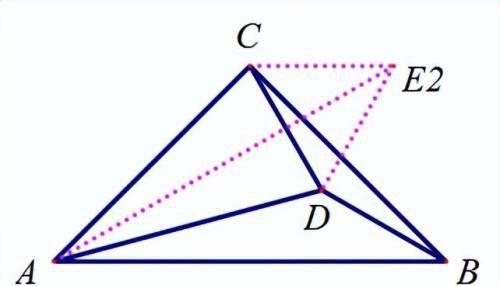
【分析】
E1--E8:证三角形全等即可得到,以下同思路的,就不再赘述。具体证明过程也比较简单,这里不再列出.
E2:这里证△ACE2≌△ADB应该是所有证全等里面难度最大的,需要计算AE2=AB.
以BC为边向两边构造等边三角形;
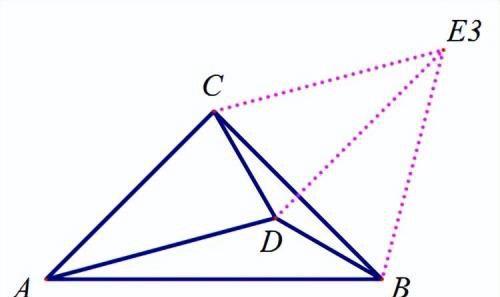
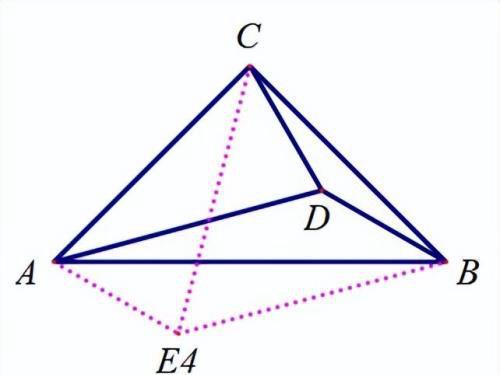
以AD、AC为边向两边构造等边三角形;
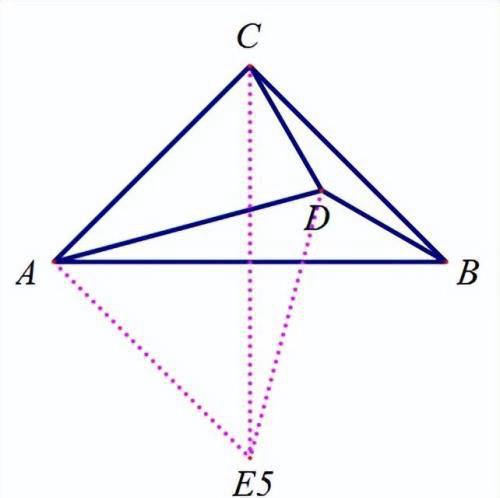
【分析】
E5,E7的证法类似,如E5,证△ABD≌△ECD,具体证明略。
以AD、AC为边向另一边做等边三角形是否成立呢?当然成立,只是它们更特殊,我们把它单独归为一类,那就是接下来的第二类.
【类二】轴对称(翻折)
由这里的∠CAD=30°,自然使我们联想到30°的2倍就是60°,所以我们自然而然的想到翻折,这里我们可分别以AD,AC为轴把△ACD进行翻折,得到等边三角形。当然这与前面直接构造等边三角形得到的图形是一致的,证明的本质也是相同的。只是轴对称(翻折)也是我们解决几何问题常用的一种思维方式,所以我们进行单列。
以AC为轴把△ACD进行翻折;
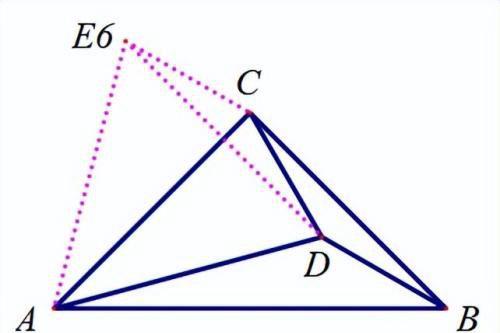
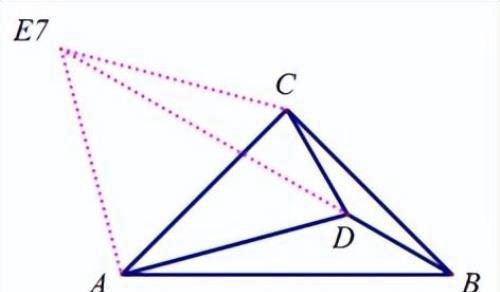
以AD为轴把△ACD进行翻折;
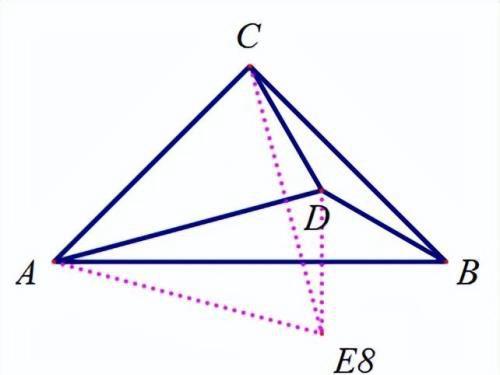
【分析】
E6,E8:这里仍然是证两次三角形全等即可得到,具体证明过程也比较简单,不再多说.
【类三】其他思路
角平分线性质定理;
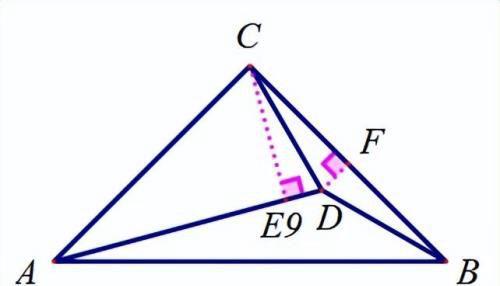
【分析】
E9:易证△CDE≌△CDF,得CE=CF,又由30°角直角三角形,易得CE=1/2AC,得CF=BF,再由三线合一即可求得结论。
作垂线,构造以AD,CB为斜边的全等直角三角形;
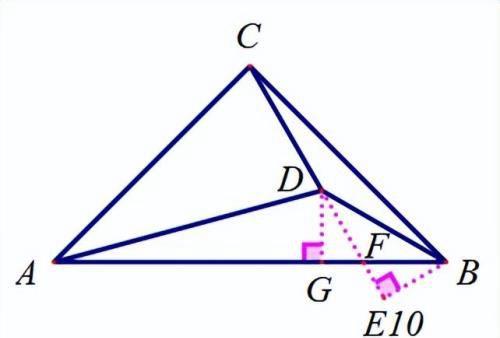
【分析】
E10:证两次三角形全等易得。
【归纳总结】
1由于题目是证明线段相等,我们容易想到等角对等边,事实上,有几种方法是可以得到15°=15°的。
2通过这道题,我们对此类题目的解法将有一个更深的认识。此题的解法应不止于此10种,欢迎大家补充。
不足之处,请君指正。
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请反馈,一经查实立刻删除内容。本文内容由快快网络小春创作整理编辑!