小波分析总结(小波分析简介)

导语：浅谈学习小波分析

"小波"就是小的波形。所谓"小"是指它具有衰减性，而称之为"波"则是指它的波动性，其振幅正负相间的震荡形式。与Fourier变换相比，小波变换是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号逐步进行多尺度细化，最终达到高频处时间细分。

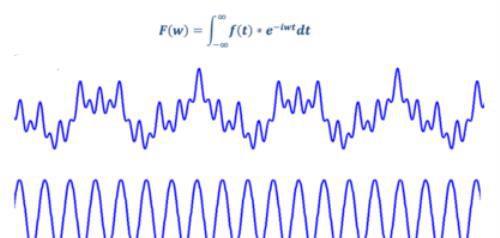
而低频处频率的细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。

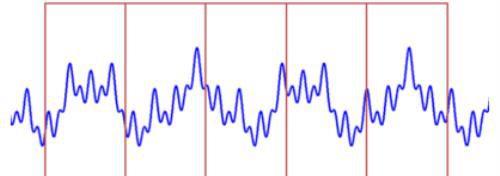
小波函数源于多分辨分析，其基本思想是将扩中的函数f(t)表示为一系列逐次逼近表达式，其中每一个都是f(t)动经过平滑后的形式，它们分别对应不同的分辨率。它可以用于边界的处理与滤波、时频分析、信噪分离与提取弱信号、求分形指数、信号的识别与诊断以及多尺度边缘检测等领域。

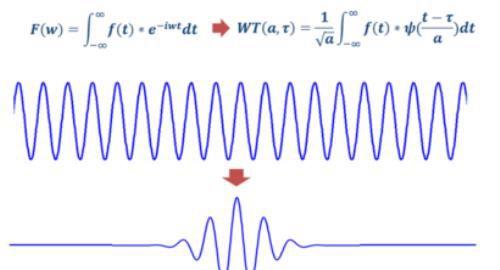
在学习傅里叶变换的时候我们接触过周期信号的傅里叶变换。傅里叶级数的直观感受就是任意一个周期信号可以用N个正余弦叠加来表示。这些正余弦的频率和幅度各异。每一个余弦信号都有着自己固定的频率和幅值。在傅里叶变换之后，对应频域上不同频率的幅值不同。

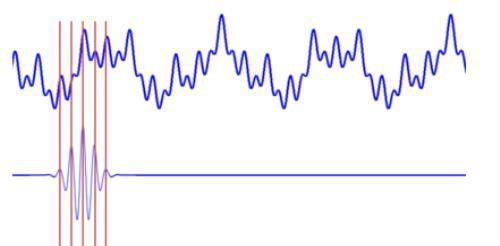
但傅里叶变换存在以下不足：

1、傅立叶变换的三种形式中的傅立叶系数都是常数，不随时间t变化，因而只能处理频谱成分不变的平稳信号。相反的，在处理非平稳信号时会带来很大误差，甚至与实际情况大相径庭。

2、求傅立叶系数是全时间域T上的加权平均，局部突变信息被平均掉了，局部突变信息的作用很难反映出来。在处理、捕捉突变信号的时候，由于差别比较大，如故障信号，导致灵敏度很差。

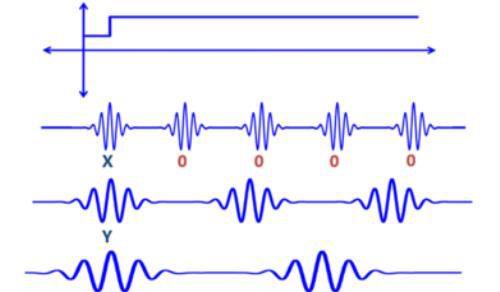
由于傅立叶变换上的不足，必须进一步改进方法，克服不足点，这就导致了小波分析的产生。小波级数是两重求和，小波系数的指标不仅有频率的指标 ，而且还有时间的指标。也就是说，小波系数不仅像傅立叶系数那样，是随频率不同而变化的，而且对于同一个频率指标，在不同时刻，小波系数也是不同的。

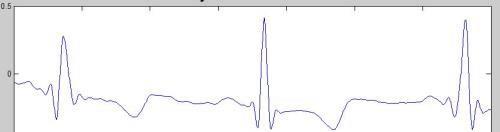
与傅立叶变换相比，小波变换是时间和频率的局部变换，因而能有效地从信号中提取信息。通过伸缩和平移等运算功能可对函数或信号进行多尺度的细化分析，解决了傅里叶变换不能解决的许多困难问题。

从图像处理的角度看，小波变换的优点：

1、小波分解可以覆盖整个频域

2、小波变换通过选取合适的滤波器，可以极大的减小或去除所提取得不同特征之间的相关性

3、小波变换具有"变焦"特性，在低频段可用高频率分辨率和低时间分辨率，在高频段，可用低频率分辨率和高时间分辨率。

4、小波变换实现上有快速算法。

小波变换的学习方法：

1. 首先对小波分析有一个大致的了解，建立感性认识。

2. 对信号与系统和数字信号处理两个领域有大致的了解。

3. 学习泛函分析，掌握相关概念，建立数学基础。认为小波分析难的人，都认为小波分析难在数学上，其真正原因是这部分学习者缺失了泛函分析方面的基础，而大部分小波分析的教程又都假设读者具备这方面的基础。

4. 开始具体的小波分析理论学习。

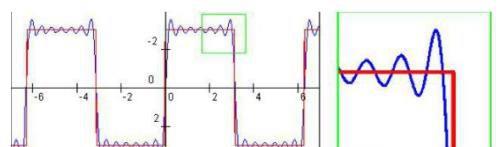
这样就对小波分析有了一定的了解，可以根据具体应用深入下去了。

从数学上讲，小波分析与傅里叶分析的原理相同，归为函数逼近，或者函数"展开"。傅里叶分析以三角函数为基底，小波分析以小波基函数为基底。三角函数的优势在于光滑性，小波基函数的主要优点是多尺度和紧支撑。

从信号处理的角度来看，傅里叶分析更适合光滑性比较好的信号，小波分析在处理奇异信号优势明显。经过多年年的沉淀，傅里叶分析与小波已经找准了各自的位置，可以尝试，但不必对任何一者的期望过高。

学习是一个漫长的过程，学习的目的要尽可能地放远，放大。学习做实验，不是非得三次就成功，而是学习知识，思考，练习，创新的过程。

慢慢的你会发现，在学习中体验到最快乐的那个点，不是最终得到结果的那一刻，而是在不断的失败中，当发现自己寻找到好的方法，或者解决掉一个难题时，那是最快乐。因为那个时刻，你在乎的不是结果，而是这个过程带给你的思考，带给你的方法，带给你的沉淀和积累。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！