高斯公式对坐标的曲面积分(高斯坐标换算)

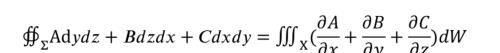
导语：「高等数学」对坐标的面积分，用高斯公式转化三重积分来计算

今天我们来讨论一下曲面积分中的第二类面积分：对坐标的面积分。

假设∑是光滑有方向的曲面，A、B、C是定义在∑上的函数并且有界，那么我们就可以得到二重积分∫∫∑ Adydz+Bdzdx+Cdxdy = lim∑(i=1,n) [A(ai,bi,ci)(△S)yz + B(ai,bi,ci)(△S)zx + C(ai,bi,ci)(△S)xy]，其中(△S)yz表示有向曲面块△S在yOz坐标面上的投影，(△S)zx表示有向曲面块△S在zOx坐标面上的投影，同理，(△S)xy表示有向曲面块△S在xOy坐标面上的投影。如果A、B、C在∑上连续，就说明二重积分∫∫∑ Adydz+Bdzdx+Cdxdy存在。

我们可以利用高斯公式来进行计算，设空间闭区间X是由分片光滑的闭区面∑围成的，函数A、B、C在空间闭区间X上都有连续一阶偏导数，闭曲面∑取外侧，则可以得到公式：

图一

补面也可以用高斯公式，如果要计算的曲面积的积分曲面∑不封闭，而且计算不方便，那么这个时候我们就可以补一块曲面∑1，使得原曲面变成封闭曲面，则可以得到：

图二

以上所讲，都是概念，我们回归标题，对于这类面积分，我们什么时候用到高斯公式来做呢。

看了这么多概念，不如直接给出一道例题，可以让大家更清晰。

图三

如图所示，当题目中给出不封闭的积分曲面∑，我们可以想到补曲面用高斯公式的方法，笔者在学习高斯公式的时候，其实也不是很理解，因此，笔者的建议是大家如果理解不了高斯公式，那干脆就背下来，毕竟曲面积分也是比较抽象的，背下来先解决题目，熟能生巧，之后再慢慢理解，我相信大家就能够理解了，笔者在做这道题的时候，其实换元法我也没想到，这是不应该的，当时还卡了好长时间，这里的y^2+z^2很明显可以用q^2来代替，这里涉及到三重积分和二重积分的基础计算，我还要再好好复习复习，这道题用直接法计算麻烦，因此用高斯公式的。

本文内容由小奈整理编辑！