二元函数的极限及极限存在的条件是什么(二元函数的极限及极限存在的条件是)

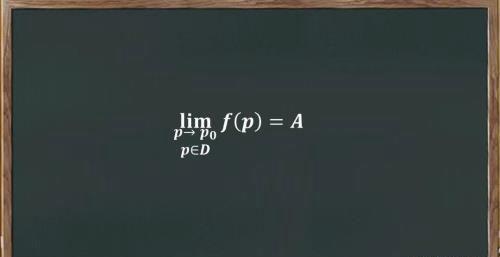
导语：二元函数的极限及极限存在的条件

二元函数极限的定义

设f是D到R上的映射，是D中的聚点。

如果对于任意一个大于零的数ε，存在一个大于零的数δ，对于任意点P∈Uº（；δ），有

∣f(P)-A∣﹤ε

则称A为P趋近于时f的极限。

二元函数极限存在的充分必要条件

定理1.设f是D到R上的映射，当P趋近于时且P为D中的点，f的极限为A的充分必要条件：对于D的任意子集E，只要是E的聚点，则

当P趋近于时且P为E中的点，f的极限为A。

证明：“充分性”显然成立，只要令E=D即可。

“必要性”因为当P趋近于时且P为D中的点，f的极限为A，

所以，对于任意ε＞0，存在δ＞0，使得对于任意点P∈Uº（；δ），有∣f(P)-A∣﹤ε

由于E是D的子集，所以

Uº（；δ）∩E是Uº（；δ）∩D的子集

又因为是E的聚点，所以当P∈Uº（；δ）∩E时

∣f(P)-A∣﹤ε

所以，当P趋近于时且P为E中的点，f的极限为A

推论1.设是D的子集，是的聚点。

推论1是定理1的逆否命题。

推论2.设和是D的子集，是和的聚点。

推论3.当P趋近于时且P∈D，极限f(P)存在的充分必要条件是：

对于E中任意满足条件不等于且趋近于当n趋近于无穷大时，它所对应的数列{f()}都收敛。

本文内容由小媛整理编辑！