矩阵相似和相似对角化有什么联系吗(矩阵相似和相似对角化区别)

导语：线性代数之相似矩阵和矩阵的相似对角化问题的方法总结

考研数学重在知识点的理解和综合应用，在做题的过程中，数学公式成为解题的重要工具。因此，扎实掌握考研数学的重点公式可以大大提高我们的做题效率。我们分章节整理考研数学线性代数部分的重点公式，旨在帮助大家理清重点，做到经常回顾，配合习题练习做到知识的灵活应用，今天我们一起了解下相似矩阵的知识点。

相似矩阵：设A,B都是n阶矩阵，若存在可逆矩阵P，使得

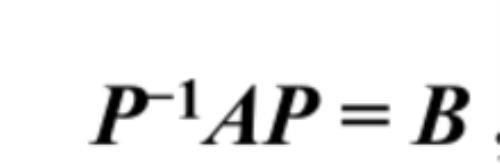
则称A相似于B。

矩阵可相似对角化的充分必要条件为：

矩阵可相似对角化的充要条件

两个矩阵相似的必要条件：

两个矩阵相似的必要条件

题型一：判定矩阵是否可相似对角化

例1：（97年考研真题)

分析：矩阵A能否相似对角矩阵的充要条件是A是否存在三个线性无关的特征向量。

解：由特征值和特征向量的定义得：

题型二：矩阵得相似标准形

例2：（矩阵相似标准形）

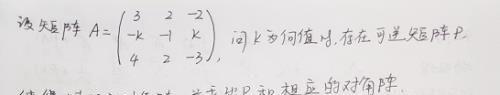
分析：A能相似于对角矩阵得充要条件是A应有三个线性无关得特征向量。

解：根据矩阵A相似对角矩阵得充要条件得：

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小滢创作整理编辑！