什么是间接证明法(间接证明的定义)

导语：什么是间接证明

什么是间接证明?

证明的方法之一是“反证法”——假设要证明的东西是假的，然后得到一个矛盾的结果。

作为第一个(非常简单的)例子，考虑证明对于正整数a和b,−4≠1。

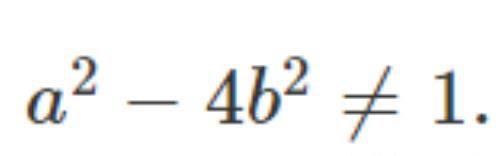
间接证明:

相反的，假设对于某些正整数a和b,−4≠1。我们有(a−2b)(a+2b)=1，这可以分为两种情况:a−2b=a+2b=1或a−2b=a+2b=−1。

在第一种情况下，两个方程相加得到2a=2，或a=1，从而得到b=0，这个解已经被拒绝了。

在第二种情况下，两个方程相加，得到2a=−2，或a=−1，即a是负数，与已知的为正数矛盾。

因此，假设被证明是错误的，这意味着它的否定——最初的命题——是正确的。

在初等数学中，“反证法”通常是证明一个条件对另一个条件是必要和充分的最简单的方法。例如，在直角三角形中，我们有勾股定理:+=。其中a和b是直角边，c是直角边。我想证明逆定理为真的情况:如果在一个边为a,b,c的三角形中:+=，那么c的对边就是直角边。假设这是假的，也就是说，c对边的角不是直角。然后我们可以竖一条垂线垂直于b，然后把a放在那条垂线上:

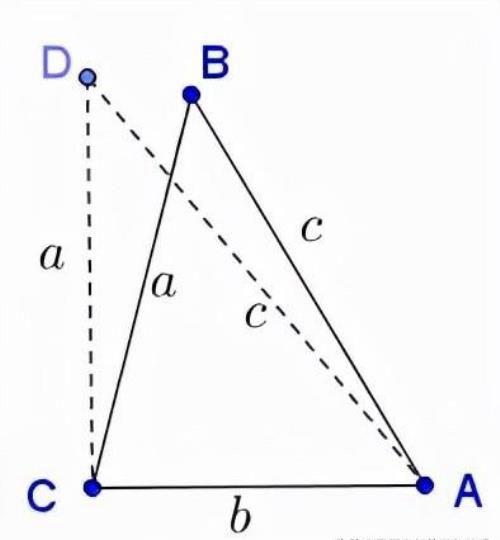
根据勾股定理，刚刚构造的直角三角形的第三条边等于c，这意味着现在有两个不同的三角形具有相同的三条边，这与SSS准则两个三角形全等相矛盾。

再举一个例子，我们知道，在同一个圆内接的边并共用同一条弧的两个圆周角是相等的。为了证明反命题，假设有两个相等的角ABC和AB &39;，C不是共圆的。这意味着B &39;位于圆外，所以CB’在D处穿过圆(当然还有其他可能性要考虑):

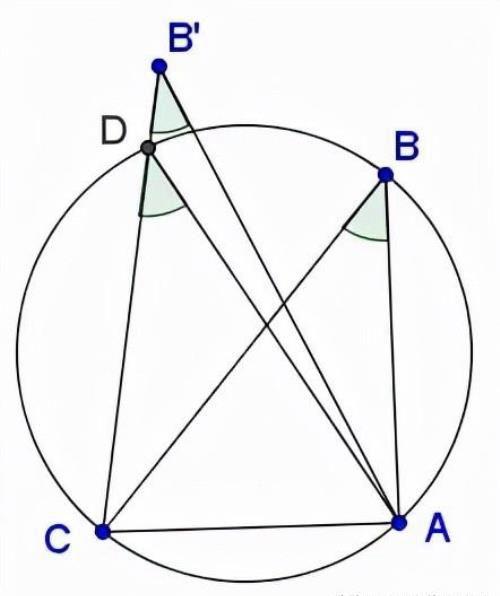
在这种情况下, ∠ADC 是三角形 ΔADB′的外角，因此：

∠ADC=∠AB′D+∠B′AD=∠ABC+∠B′AD>∠ABC.

但这与∠ABC和∠ADC是在同一个圆内的事实相矛盾，根据同一圆弧上的圆周角定理，它们应该相等。

另一个典型的例子是用反证法证明是无理数。

证明：假设是有理数，可以写成=p/q, 即=2，这个等式告诉我们p是偶数。假设p和q互为素数，q必然是奇数。然而，偶数的平方能被4整除，这使我们得出q是偶数的结论(可令p=2k就可证得）。这是与p和q互为素数相互矛盾，所以不是有理数。

反证法的三个步骤:

假设陈述是错误的。利用错误的假设推导出一些根本不成立的东西，比如矛盾或不真实的情况。根据发现的与公理或定理相谬误的矛盾，那么间接证明原始的陈述一定是正确的。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小苹创作整理编辑！