导语：初中数学里的绝对值，你以为这概念简单，它说你年轻，太草率了！

一直很疑惑，直角坐标系里面的交点到底是数字“0”，还是字母“O”？

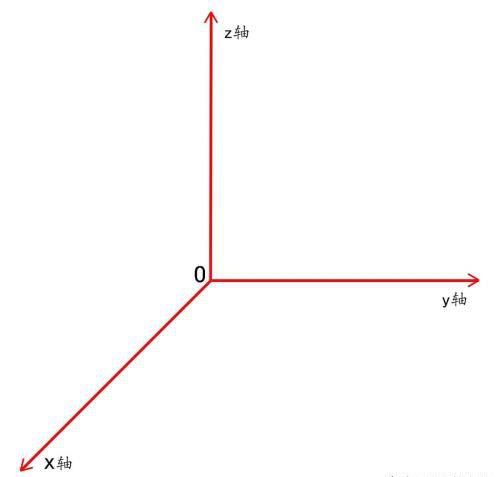
笛卡尔坐标系

从坐标系来说，笛卡尔直角坐标系（Rectangular Coordinates）的三要素是：零点、正方向、单位长度；这么看应该是0（零）；

从这个原点的翻译来看是：origin，按照数学的命名习惯，取自于这个词汇的首字母：O；

这么看应该取字母O更符合这个概念的发源。

说原点，是为了更好说明绝对值服务。

1. 绝对值还很年轻，不到200岁！

绝对值是初中数学中最重要的概念之一。

1）绝对值概念的提出者

提起绝对值的产生，就需要从“现代分析学之父”的德国大数学家魏尔斯特拉斯(Weierstrass，1815-1897)说起，他于1841年提出绝对值的定义，距今不到200年的历史。

顺带说下，生于1707年，逝于1783年把无穷级数玩得贼溜贼溜，写出了数学史上最多论文的大神欧拉，一生未接触过绝对值。

魏尔斯特拉斯

2）绝对值的定义

来让绝对值勾起下大家的回忆，不是想起那知了声声叫着夏天，也不是隔壁班走过窗前的姑娘，是想起绝对值的定义：

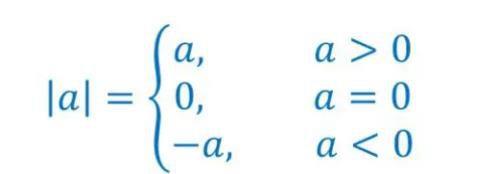
绝对值定义

到后来，又学习了它的几何含义，|a-b|表示的就是在数轴上点a和点b之间的距离：

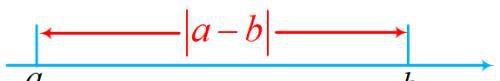
而|a|可以看成是|a-0|，因此它表示的就是数轴上点a和原点的距离。

通过几何含义来看，体现出了几何方法的优越性，极其直观，一目了然。

从这一刻开始，绝对值就自然和距离联系在一起，并将距离赋予了绝对值，以表示其意义。

3）绝对值的性质

我们就很容易总结出其满足的以下3条性质关系：

（1）任意的数的绝对值都非负；

（2）任意两个数乘积的绝对值等于两个数的绝对值的乘积；

（3）两个数的和的绝对值不会大于这两个数的绝对值的和；

我们用数学符号翻译出来就是：

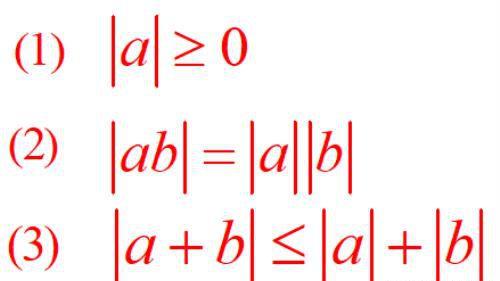
2 向量

1）平面向量

到了高中之后，我们又学习到了一个全新的数学对象：平面向量。一个既有大小又有方向的家伙。

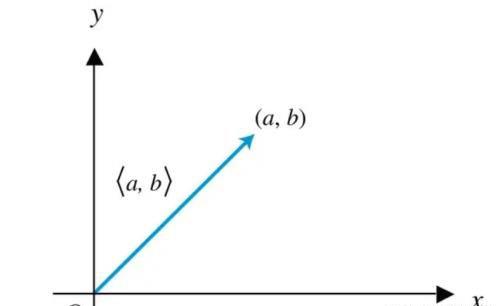
向量最通俗的几何解释就是带有箭头的线段，它既有长度，也有方向。

我们把向量放到直角坐标系里边来研究，把每一个向量的起点都平移到坐标原点，于是就可以用它的终点坐标来表示一个向量

向量的长度我们一般称之为模长，用符号|V|来表示，在直角坐标系里，将平移到以原点为起点的向量的横纵坐标建立直角三角形，根据勾股定理，可以得到一个向量模长公式：

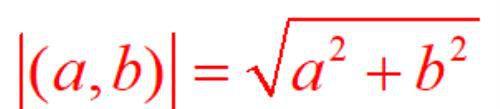
2）三维空间向量

对于在高中选择性必修课本里，引入了空间向量，即：三维向量

定义了三维空间向量的模

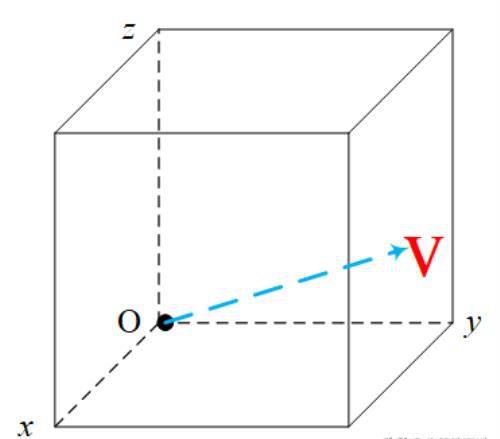
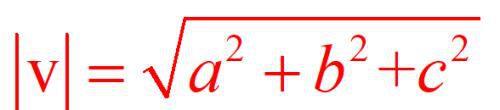
从几何图形上看，绝对值表示的就是距离，而且是到原点的距离。

向量的模长就是绝对值的意思，从二维关系推导到了三维空间，从面到体，不过还是那些数学的味道，不仅如此向量模长还是距离，而且所满足的性质跟数的绝对值所满足的性质几乎完全一致。

3 复数

在高中我们还重点研究了另外一个概念——复数。

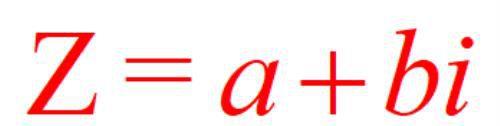
复数

其中a和b都是实数，i为虚数单位，通俗地讲就是-1开平方后一个根。实数(b=0)和纯虚数(a=0,b≠0)都是复数的特例。

其意义在复平面的表示如图所示，可以发现其长度和平面向量的长度表示完全相同。

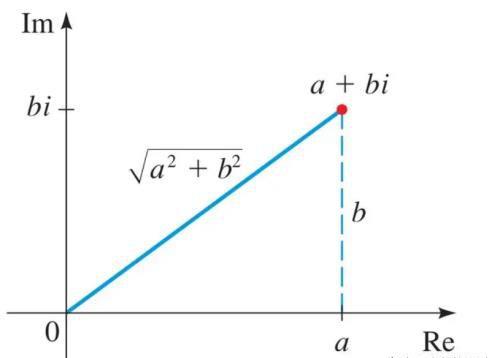
绝对值的符号又一次在这里表示距离。

我们会总结出：实数的绝对值，向量的模长，复数的模长，三者从本质上都一样的。

4 绝对值概念的统一

绝对值的概念，这是初中数学中的难点之一，由学习有理数运算法则的需要而引入；

到学习二次根式时，又由于如下的关系，与算术根联系起来;

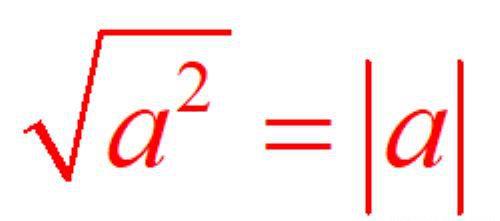
到初三，在方程与不等式中又再次出现，；

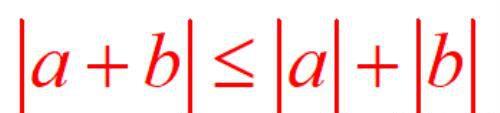
在直角坐标系中，因为如下关系，它又是两点间距离公式的特例，

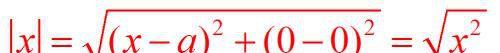
到高中，学习了函数知识后，还可以把实数的绝对值规定为如下关系：

在复数里复数的模又可以理解为实数的绝对值概念的推广。

数学中多数概念都是在教学进程中不断扩展的，绝对值这一概念，在中学数学中通过梳理就有以下扩展路径:

有理数绝对值 一> 实数绝对值 一> 绝对值与算术根一> 平面向量的模 一> 空间向量的模一>复数的模（绝对值）

教学中还可以把绝对值与数轴上两点间的距离以及与平面上两点间的距离联系起来，也可以将这个用新的函数形式来表达。

当然也可以安排一堆的练习，来加深学生对绝对值认识的不断发展以及深入理解

绝对值练习题01

绝对值练习题02

5 绝对值概念 后来的成长

进入20世纪以来，数学逐渐从研究具体的概念对象，转为研究抽象的形式对象，从而逐渐走上了抽象化与公理化的道路。

数的绝对值，向量的模长，复数的模长，本来是三个不同的研究对象，但是他们之间具有相同的特征满足：

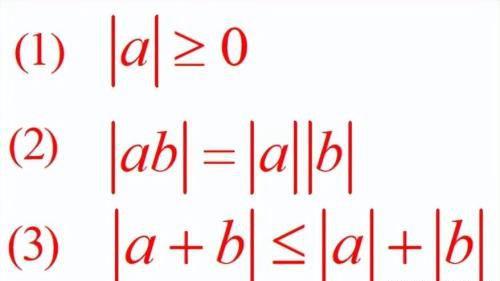
因此数学家就提出：假设有一个东西，它满足上面三条性质，那么我们就可以把这个东西定义为一个新的研究对象，这个新的研究对象叫“范数”(norm)。

因为这个东西的思想源于绝对值，但又比绝对值高级的不止一丢丢，所以数学家们又发明了一个新的符号来表示：||a||，这家伙不是绝对值的绝对值哈！

有兴趣可以去查看一下范数的具体定义。

在数学的花园里，有很多也满足上面三个条件。因此对于其它的数学对象，我们也可以有范数。甚至于，对于同一种数学对象，我们可以有好几套不同的范数，比如内积就满足。

这个内容已经超出了初等数学的范围，就不再这里做进一步的探讨了。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小璎创作整理编辑！