证明不等式的题目(证明不等式的方法总结)

导语：一道初中几何题-证明不等式的成立

一道初中几何题-证明不等式的成立

在凸四边形ABCD中，∠DCB=90°，E是AB的中点，证明2CE<AD+BD.

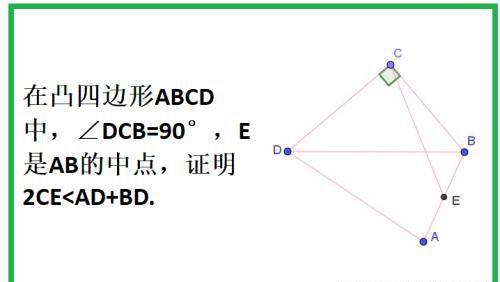
证明1： 如图，去BD中点O， 连接CO和EO，

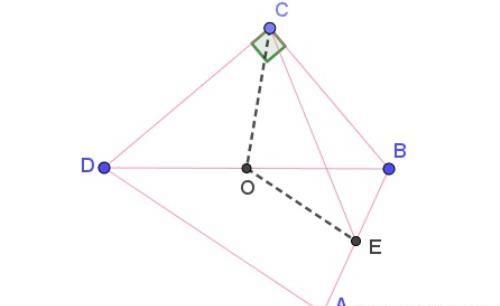
因为∠BCD=90°，因此斜边中线为斜边的一半，CO=BD/2,

而EO是三角形ABD的中位线，所以EO=AD/2,

在三角形COE中有， CE<CO+EO

即CE<BD/2+AD/2

因此证得：

2CE<BD+AD

证明2：如图延长BC至B’,使得BC等于B’C,连接B’D

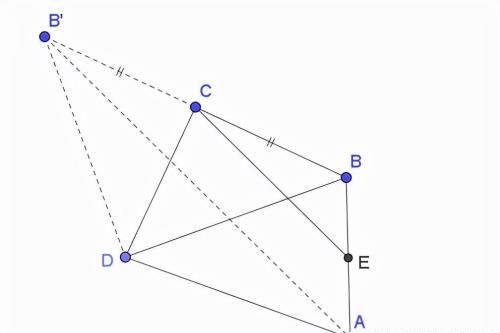
显然CE为三角形ABB’的中位线， 因此

CE=B’A/2, 即B’A =2CE

而在三角形ADB’中， B’A<DA+DB’

但由于B’是B的对称镜像点，DB‘=DB

所以 2CE<AD+BD

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小德创作整理编辑！