二重积分变积分限怎么求导(二重积分计算中的积分限的确定)

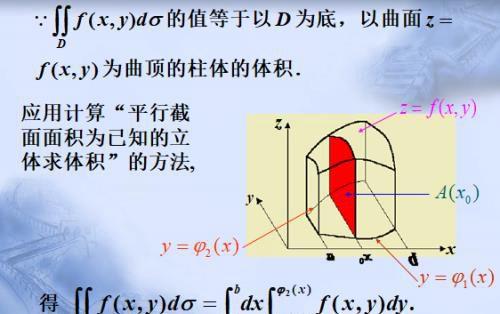
导语：二重积分的积分限变换问题

对于二重积分：

积分过程分为先对y积分或者先对x积分。如果先对y积分，则在对y积分的时候，x就是常数，所以y的积分限可以由x（包括其它常数）来表示：

这样做的目的，就是为了把上式变成x的函数，以便第二次对x积分的时候可以得出具体的结果。反过来，如果先对x积分：

那就把x的积分限用y的函数表示。

如果是必须改变积分次序的情况，则要考虑是否要进行积分区域的分割问题：

改变积分次序以后：

这里注意应该注意的地方是，当改变成先对y积分以后，积分的上限和下限都必须是同一个关于x的函数。

上图中，我们看到，曲线M和直线N明显不能用同一个函数表示，这个时候就用一条沿着Y轴的直线对积分区域进行分割，分割以后，曲线M和直线N就可以分别用x的函数表示，这样就可以积分了。

同样，如果先对x积分，必要的时候就用横线进行分割：

上图中，先对x进行积分的时候，对于绿色积分区域，用横线y=a将积分区域分成了三块。

简单来说：

1：当先对y积分时，就把x看作常数，因此积分限可以由x和其它常数表示，反之亦然。

2：当先对y积分的时候，如果积分限不能用同一个关于x的函数表示，则用竖线分割积分区域；如果先对x积分则用横线分割。

本文内容由小玥整理编辑！