线性代数中逆矩阵的运算规则(逆矩阵是啥)

导语：线性代数的秘密：逆矩阵的意义是什么？（上）

今天，笔者给大家讲讲逆矩阵的意义，这个话题篇幅较长，需要分成好几次来聊，话不多说，让我们开门见山。

什么是逆矩阵呢？它的精髓包含在一个公式里，今天我主要带大家理解下面这个公式。大家先瞅瞅它，（看不懂完全没关系。先简单留个印象就行了)。等你看懂了它，你就明白了逆矩阵的意义。

式中A是矩阵，A的负1次方表示逆矩阵

好了，让我们开始今天的线代之旅，有请我们的明星矩阵：

我们上次的文章中给大家讲了矩阵乘法的意义。（强烈建议大家先看笔者的前一篇文章，介绍矩阵相乘的本质）这种二维矩阵在空间中可看成是一个以i’（1，3），j’（2，4）为基底的倾斜坐标系：

大家仔细观察这个图

这个斜坐标的基底不是i和j，它是两个维度复合而成的：

和直角坐标系对应的矩阵是什么呢：

于是，逆矩阵说话了：我逆矩阵可以把这个斜的坐标系变回我们常见的直坐标系：

看到这里，你大概就明白了，逆矩阵为什么叫逆矩阵呢？因为大部分矩阵可以把直角坐标系变成各种斜的坐标系，而逆矩阵却可以把斜的坐标系变回直角坐标系。

矩阵和该矩阵的逆矩阵复合在一起同时操作我们直角坐标系，最终等于没有作用（两个作用相互抵消了）:

这个大写I的意思是单位矩阵，这个单位矩阵其实就表示我们的直角坐标系那两个基向量i，j。

现在问题来了：

如何求这四个问号呢？我们直接设a,b,c,d四个未知数不就完了嘛:

挨个对应解得：

这个逆矩阵A^-1张什么样子呢:

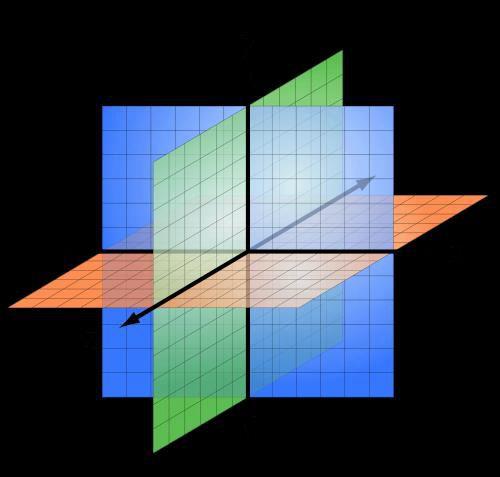
类比空间，你是不是很快就想到了：逆矩阵作用就是把斜的三维xyz坐标系变回我们常见的直角三维坐标系。

不过，求三阶矩阵的逆矩阵用方程去解就非常复杂了，不信你可以试试看。应于这个问题，我将给大家介绍更多好玩的数学工具，这个安排到下一篇讲。

最后给大家留个问题：你能求下面这个矩阵的逆矩阵吗？

（未完待续）

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小若创作整理编辑！