导语：二进制数值数据的运算方法

补码加法与减法的运算规则

加减法运算是计算机中最基本的运算，通常选用补码实现，实现的算法是：

[X+Y]补= [X]补+ [Y]补 MOD 2 (2.6)

[X-Y]补= [X]补+ [-Y]补 MOD 2 (2.7)

例如， X =+0.1010， Y = -0.0101，则:

[X]补= 01010， [Y]补= 11011，[-Y]补= 00101 [X]补+ [Y]补 MOD 2= 01010+11011 = 100101 ，按2取模后的结果为00101，其真值为 +0.0101，符号位与数值位均正确。

[X]补+ [-Y]补 MOD 2= 01010+00101 = 01111 ，按2取模后的结果为01111，其真值为 +0.1111，符号位与数值位均正确。

在执行补码加减运算时，仅在其运算结果不超出机器能表示的数值范围时，运算结果才是正确的，否则就是“溢出”，得到的结果是错误的。执行补码加减法运算一定要检查溢出，检查是否溢出有3种思路。

（1）检查参与运算的数据和结果的符号是否正确。正数加正数结果为负、或者负数加负数结果为正，都是溢出。

（2）为了方便判别溢出,某些机器采用模4补码（即使用双符号位）,其定义为：

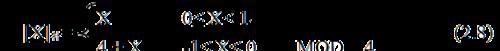
例如，X=+0.1011，[X]补=001011， X=-0.1011，[X]补=110101，每个补码都使用两个符号位，而且两个符号位总是同值。在执行加减法运算时，若结果的两个符号位相同，为00或11表示结果正确；当符号位为01或10时，表示数值溢出。

（3）数值位产生向符号位的进位，而符号位不产生向更高位的进位，或数值位不产生向符号位的进位，而符号位却产生向更高位的进位也是溢出。这很容易用数值位的进位输出与符号位的进位输出的“异或”操作来判断。

源码一位乘法的运算算法

原码一位乘法是将符号位与数值位分开进行运算，乘积的符号是两个数符号的异或值，数值是两个数绝对值（即原码表示的数值位）的乘积。

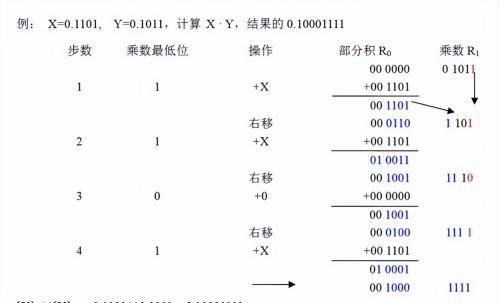
例： X=0.1101, Y=0.1011，计算 X × Y

手工计算时，是根据乘数的每一位求部分积，各部分积依次左移一位，最后一次总加求和的办法得到乘积结果，再用负乘负、正乘正为正，负乘正、正乘负为负的方案来处理符号。到了计算

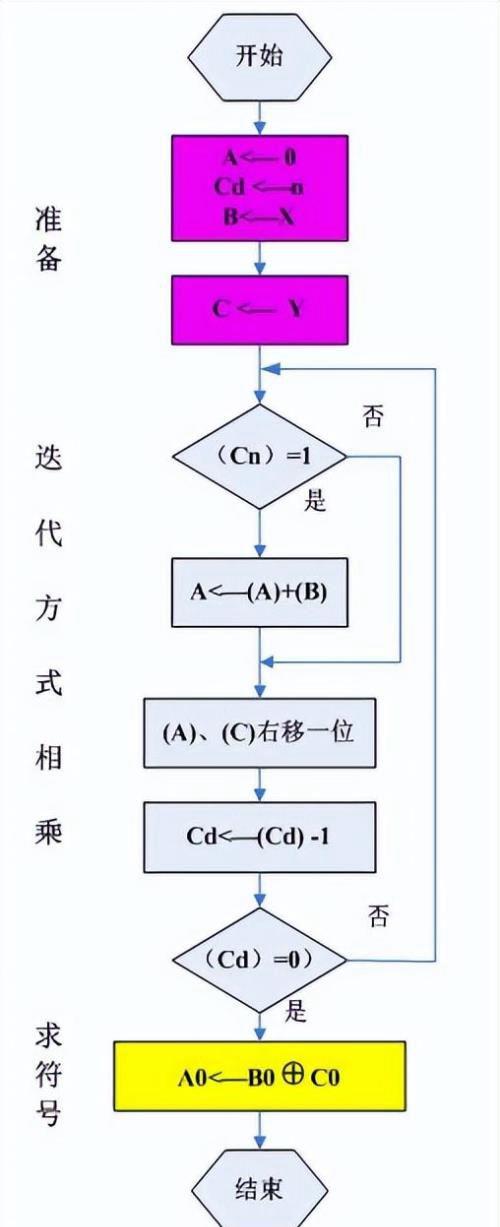
（1）将部分积的一次总加改为分步累加；　　（2）将部分积左移改为部分积右移；　　（3）使部分积连同乘数一起右移，以便保存双倍位数的乘积。　　原码一位乘法的算法是：

（1）用乘数寄存器的最低位选择求部分积的数据来源：被乘数或0值；相加求得部分积并使其右移一位，乘数也同时右移一位，此时高位部分积的最低位移入乘数寄存器的高位。　　（2）用一个特定的寄存器控制相乘次数（决定于数据位的位数）。　　（3）用乘数与被乘数符号位的异或值作为乘积的符号。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小馨创作整理编辑！