二叉树详解(二叉树结构图)

导语：两分钟读懂二叉树（Binary Tree）

一、二叉树（Binary Tree）的简介

在计算机科学中，二叉树是一种树形的数据结构，其中每个节点最多具有两个子节点，其被称为左子节点和右子节点。仅使用集合理论概念的递归定义是（非空）二叉树是一个元组（L，S，R），其中L和R是二叉树或空集，S是单例集合。

树中的常见术语包括：

某个节点的深度是指当前节点到根节点的边的个数某个节点的高度是指当前节点到最深的叶子节点的边的个数树的高度是指根节点的高度

树结构的优点包括：

反应了数据的关系具有层次结构表达能力高效的插入和搜索灵活的数据结构，允许以较小的代价移动子树

如下图所示就是一个二叉树：

在计算机领域，二叉树有两个主要的用途：

第一个用途是用来实现二叉查找树和二进制堆，以便于搜索和排序。

第二个用途是作为具有相关分叉的数据表示。例如霍夫曼编码（Huffman coding）和分支图（Cladograms）。

注意二叉树并不是一种数据结构，它是一类数据结构。在二叉树数据结构中，不平衡的树比自平衡树的效率低很多。平衡与否取决于左右两个子树的高度差的绝对值。绝对值小于1的一般可以理解为平衡树，否则是不平衡树。

二、二叉树（Binary Tree）的分类

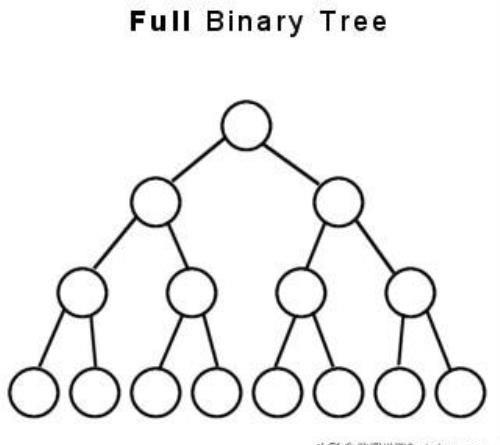
满二叉树（Full Binary Tree）

如果一个二叉树的每一个节点数都是最大节点数，那么它就是满二叉树。如下图：

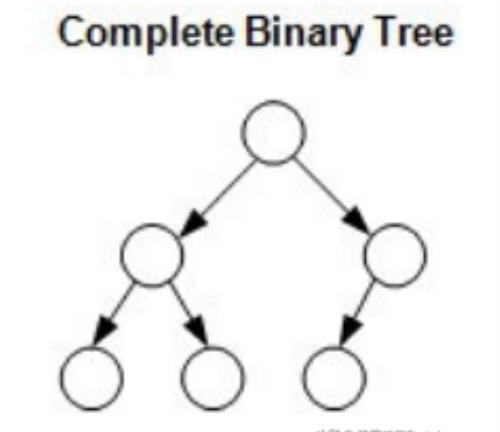
完全二叉树（Complete Binary Tree）

如果一个二叉树除了最后一层外的每一个节点数都是最大节点数，那么它就是完全二叉树。如下图：

二叉树的性质

满二叉树的节点数是2^k-1

完全二叉树的节点数2^{h-1} \leq k < 2^h-1

三、二叉树（Binary Tree）的应用

二叉树是一种非常基础的数据结构，它和它的变种有很多的应用。这里列举一些：

二叉查找树（Binary Search Tree）：二叉查找树是一种具有高效查找效率的树形结构，在搜索中应用非常广泛。霍夫曼编码树（Huffman Coding Tree）：这压缩算法中应用广泛，例如JPEG和MP3格式的文件压缩。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小涵创作整理编辑！