独立性卡方检验怎么使用(卡方独立性检验结果分析)

导语：管理心理学之统计（24）独立性的卡方检验

卡方也可以被用于检验两个变量间是否存在关系。这种情况下，样本中的每个个体被归入两个不同的变量，通常用矩阵表示。行与一个变量类别相对应，列与另一个变量类别相对应。矩阵的每个单元中的数字表示特定组的频数。

1.独立性检验的虚无假设

独立性卡方检验的虚无假设为：被测量的两个变量是独立的。这个假设可以被分成两个不同的概念形式

A. 数据被看作一个样本，每个个体都有在两个变量上的测量值。例如，H0：对于学生的一般总体，在颜色喜好与性格之间不存在关系。相关需要的是X与Y的数值分数，只使用将个体归入类别的频数。

B. 数据被看作两个（或多个）独立的样本，代表两个（或多个）分开的总体。卡方检验的目的在于确定总体间是否存在显著的差异。例如H0：在学生的总体中，性格内向的人的颜色喜好分布于性格外向的人的颜色喜好分布之间不存在显著差异。两个分布有相同的形状和相同的比例。

虽然形式不同，但这两种概念形式之间具有等价性。备择假设H1认为总体有不同的比例。例如H1：性格内向的人的颜色喜好分布与性格外向的人的颜色喜好分布之间存在差异。

2. 观察频数与期望频数

独立性卡方检验使用与拟合度检验一样的基本逻辑。样本分布频数被称为观察频数f0。期望频数fe的计算公式为：

其中fc是列总和，fr是行总和。期望频数的具体计算如下表：

3. 卡方与自由度

独立性卡方检验使用的公式与拟合度卡方检验是完全一样的

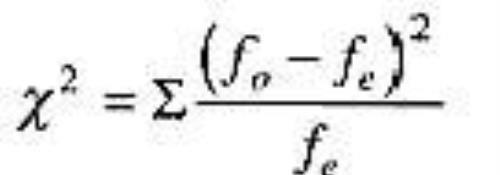
独立性卡方检验的自由度df基于可以自由地选择期望频数的单元个数。由样本大小，数据的行总和列总共同决定。公式为df=(R-1)(C-1)。

4. 独立性卡方检验，皮尔逊相关，独立测量t假设检验的相似性

假定研究者在调查十岁儿童的学习成绩与自尊之间的关系。

A. 如果研究者得到两个变量的数值，那么得到的数据可以计算皮尔逊相关，描述的是学习成绩与自尊之间的关系的程度与方向。数据形式如下：

B. 如果研究者将学习成绩归为两个类别：高与低，然后使用每个个体自尊的数值，那么得到的数据适用于独立测量t检验，检验将用于确定成绩高的人与成绩低的人的自尊是否存在显著差异。数据形式如下：

C. 如果研究者将个体的两个变量都归入类别，得到的数据为频数分布，那么适用于卡方检验。数据形式如下：

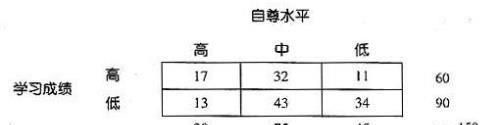
皮尔逊相关，独立测量t检验与独立性卡方检验都是为同一个目的服务的，都是要评估两个变量间的关系。因此独立性卡方检验可以被看做是另外两个统计过程的替代方法。

参考书目：行为科学统计，现代心理与教育统计学

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小碧创作整理编辑！