导语：三角形的五心是三线共点的产物，聊一聊初中数学共点线的证明思路

共点线的证法

1、意义

共点线在初等几何中,很常见,因为体现三角形重要属性的五心——重心、垂心、外心、内心和旁心,全是三线共点的产物。由此可见:共点线是反映图形特性的一种重要方式。另一方面,许多共线点,摇身一变就是共点线,例如,上一篇文章中最初的例1,实际上也就证明了如下一个共线点。

T1和T2是内接于同一圆的两个三角形,同时T1的顶点恰是T2各顶分成的三段弧之中点。

求证T1与T2所围成的六边形中,三双对顶的连线共点。

（这也是苏联的一道赛题,因为在上一篇例1中已证这三线都过内心,故实质上证出了六线共点。）

反之,共点线又常常化为共线点,所以,它们在几何中犹如一对孪生的姊妹,事实上,它俩在射影几何中,正是互为对偶的图形。

2、基本思路

（1）证其中二线的交点在第三直线上,这又有两种等价形式：

交点与第三线上某点的连线重合于第三线

交点与第三线上某两点共线

（2）证明各线都过某个定点

（3）归结为已知的共点线,例如垂心可化为外心

（4）利用判定共点线的有力工具-西瓦(Ceva)准则

2、证法举例

例1、已知直径为AB的半圆和半圆周上另一点X,设tA、tB和tX分别是此圆在A、B、X处的切线,设Y和Z分别为两对直线tB、AX和tA、BX的交点（如图1）。

求证：三直线YZ、tx、AB共点或平行。

图1

分析：题中相切、平行和垂直(直径所对圆周角)都是很好利用的条件。

证法1：证交点在第三线上(1)

首先，容易看出:当YZ∥AB时,ABYZ为矩形,相应的,X为半圆弧的中点,故tX∥AB,即这时三线平行。

若 YZ不平行 AB,设它们的交点为W,而tX与tA、tB的交点顺次U、V,则有B

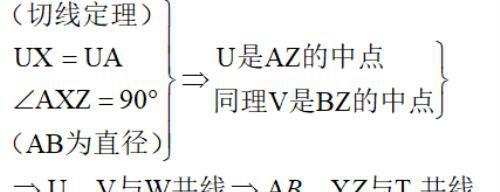
证法2证交点在第3线上(2)

假定W是tx与AB的交点,再证它在YZ上,因与上类似,故不再重复。

本例亦可用下面的西瓦准则证明

4。一个有力的工具—西瓦(Gera)准则

在前面,我们曾介绍了判定共线的一个非常有效的工具——梅氏准则。这段又称共点线与共线点,犹如一对姊妹,按此理度之,在共点线中也该有一个类似的得力工具,事实也正是这样,即有

(1)西瓦准则

准则:在△ABC中,设X、Y、Z依次在三边BC、CA、AB或446·其延长线上,则AX、BY和CZ共点或平行的充要条件是

（2）应用举例

对三角形的五心,皆可用西瓦准则证之。其中,内、旁、重、诸心与之相应的三线,分原三角形各边之边比皆为已知,故就原三角形运用西瓦准则,皆可轻易证之。至于外心,因它所共之三线不是发自三角形的顶点,故还需转化成垂心,敌以它为例,说明如何运用西瓦准则,较有启发作用。

例2、三角形的三条中垂线交于一点。

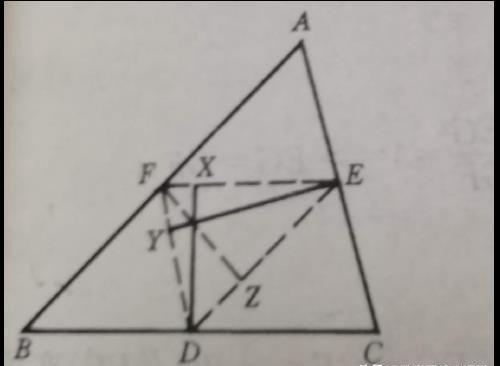
图2

证明：设D。E。F依次为AABC各边之中点（如图2所示），连结DE、EF、FD,再设△ABC各边的中垂线与△DEF相应(平行)之边的交点分别为X、Y、Z,则有

注1：△ABC的外心,实为△DEF的垂心,故本例实际上也用西瓦定理证了三垂线共点。

注2：对于外心,用中垂线的等距性极易证之,这里仅借以说明西瓦准则应用的广泛性。

除了共点线，西瓦定理(心要性)还可以用来证线段相等比例、平行行等问题。试着下题。

已知在四边那ABCD中,两组对边延长后的交点为E、F, EF//BD，延长AC交EF于G。求证：EG=GF.

说明： 这是1978年全国数学竞赛第二试的第1题、当年公布的答案是巧妙的引了一条平行线EH// BF,如图3,然后证出CEHF是平行四边形，从而使问题得证。

图3

现用西瓦定理,则不引等助线即可证之如下,

多么简捷!不但如此,其逆命题(EG =GF =＞ BD// EF)亦可由西瓦定理证明。

在例1中,仍设W是YZ与AB的交点,则就△AWZ应用西瓦定理,不难证明。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小故创作整理编辑！