导语：透彻分析批归一化Batch Normalization强大作用

在深度神经网络训练中，Batch Normalization有诸多非常强大的作用和效果：无论使用哪种激活功能或优化器，BN都可加快训练过程并提高性能；解决梯度消失的问题；规范权重；优化网络梯度流...等等。

批量归一化（BN）是神经网络的标准化方法/层 通常BN神经网络输入被归一化[0,1]或[-1,1]范围，或者意味着均值为0和方差等于1。 BN对网络的中间层执行白化

本文只关注BN为什么工作的这么好，如果要详细理解BN详细算法，请阅读另一篇文章《批归一化Batch Normalization的原理及算法》，本文从以下六个方面来阐述批归一化为什么有如此好的效力：

（1）激活函数

（2）优化器

（3）批量大小

（4）数据分布不平衡

（5）BN解决了梯度消失的问题

（6）BN使模型正则化

为什么需要归一化？

通过使用BN，每个神经元的激活变得（或多或少）高斯分布，即它通常中等活跃，有时有点活跃，罕见非常活跃。协变量偏移是不满足需要的，因为后面的层必须保持适应分布类型的变化（而不仅仅是新的分布参数，例如高斯分布的新均值和方差值）。

神经网络学习过程本质上就是为了学习数据分布，如果训练数据与测试数据的分布不同，网络的泛化能力就会严重降低。

输入层的数据，已经归一化，后面网络每一层的输入数据的分布一直在发生变化，前面层训练参数的更新将导致后面层输入数据分布的变化，必然会引起后面每一层输入数据分布的改变。而且，网络前面几层微小的改变，后面几层就会逐步把这种改变累积放大。训练过程中网络中间层数据分布的改变称之为："Internal Covariate Shift"。BN的提出，就是要解决在训练过程中，中间层数据分布发生改变的情况。

减均值除方差：远离饱和区

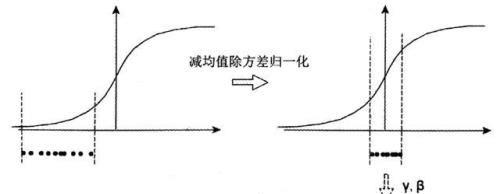
中间层神经元激活输入x从变化不拘一格的正态分布通过BN操作拉回到了均值为0，方差为1的高斯分布。这有两个好处：1、避免分布数据偏移；2、远离导数饱和区。

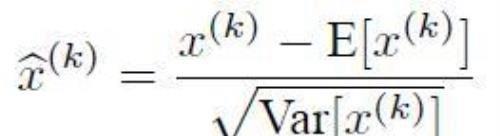
但这个处理对于在-1~1之间的梯度变化不大的激活函数，效果不仅不好，反而更差。比如sigmoid函数，s函数在-1~1之间几乎是线性，BN变换后就没有达到非线性变换的目的；而对于relu，效果会更差，因为会有一半的置零。总之换言之，减均值除方差操作后可能会削弱网络的性能。

缩放加移位：避免线性区

因此，必须进行一些转换才能将分布从0移开。使用缩放因子γ和移位因子β来执行此操作。下面就是加了缩放加移位后的BN完整算法。

激活函数

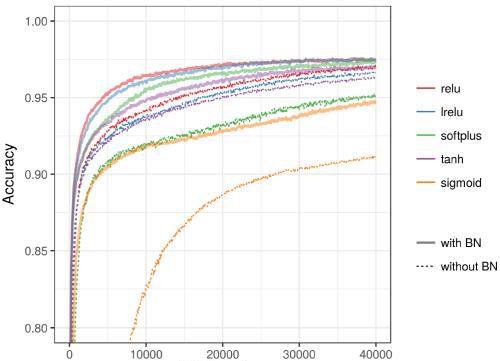
在所有情况下，BN都能显著提高训练速度

如果没有BN，使用Sigmoid激活函数会有严重的梯度消失问题

如下图所示，激活函数sigmoid、tanh、relu在使用了BN后，准确度都有显著的提高（虚线是没有用BN的情况，实线是对应的使用BN的情况）。

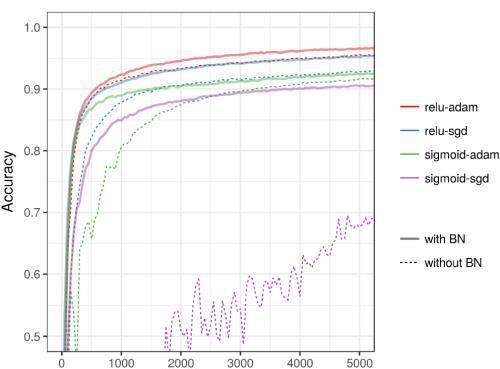
优化器

Adam是一个比较犀利的优化器，但是如果普通的优化器 ,比如随机梯度下降法，加上BN后，其效果堪比Adam。

ReLU +Adam≈ReLU+ SGD + BN

所以说，使用BN，优化器的选择不会产生显着差异

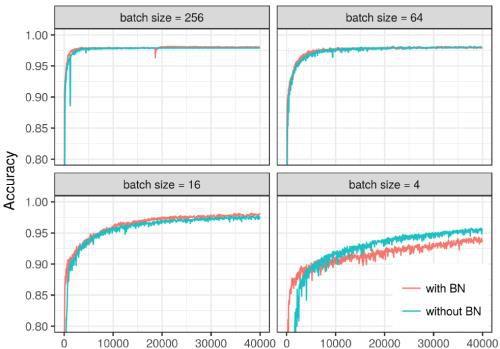
批量大小

对于小批量（即4），BN会降低性能，所以要避免太小的批量，才能保证批归一化的效果。

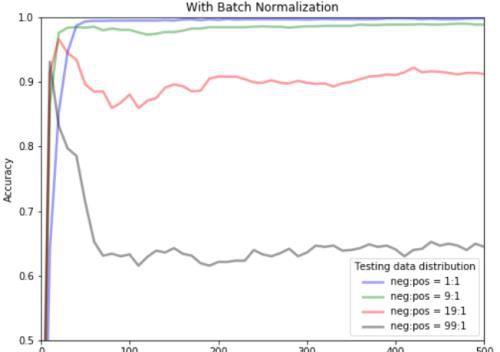
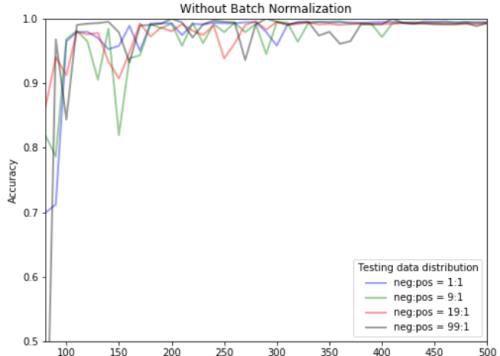
数据不平衡

但是，如果对于具有分布极不平衡的二分类测试任务（例如，99：1），BN破坏性能并不奇怪。也就是说，这种情况下不要使用BN。

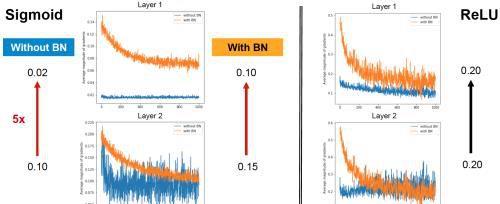
BN解决了梯度消失的问题

如下图所求，BN很好地解决了梯度消失问题，这是由前边说的减均值除方差保证的，把每一层的输出均值和方差规范化，将输出从饱和区拉倒了非饱和区（导数），很好的解决了梯度消失问题。下图中对于第二层与第一层的梯度变化，在没有使用BN时，sigmoid激活函数梯度消失5倍，使用BN时，梯度只消失33%；在使用BN时，relu激活函数梯度没有消失。

BN使模型正则化

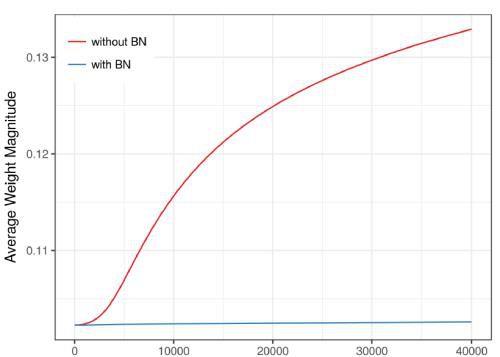
BN算法后，参数进行了归一化，不用太依赖drop out、L2正则化解决归 一化，采用BN算法后可以选择更小的L2正则约束参数，因为BN本身具有提高网络泛化能力的特性。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小梓创作整理编辑！