小升初数学分数裂项简便方法(分数裂项是什么意思)
导语:小升初数学|分数裂项深度剖析
分数裂项是小升初数学中计算板块一个重要内容,今天本人将结合我的备课内容来为大家深度剖析一下这部分内容。
在学习分数裂项知识前,我们需要掌握的第一个知识就是什么样特点的分数可以裂项?什么是分数裂项?带着这些疑问,我们先来看一下下面几道算式:

图1
图1中的4道算式都有一个共同的特点,通过观察,我们不难发现:
1⃣️计算结果的分子是原来两个分数分母的差,简言之,我们可以把这个特点描述为“子差”;
2⃣️计算结果的分母是原来两个分数分母的乘积,简言之,我们可以把这个特点描述为“母积”
以上规律,用字母表示,如图2所示:
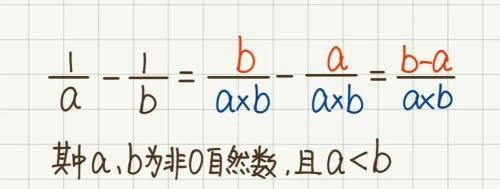
图2
进一步观察,如果我们将图2中的式子倒过来观察,式子也是成立的(如图3所示):

图3
像图3这样,一个符合“母积子差”的分数,可以利用同分母分数减法计算的原理(见图4)将一个分数裂项变成2个分数相减的形式(即“变1为2”,这就是本期为大家介绍的分数裂项中的裂差知识(补充说明:“裂”体现在“变1位为2”;“差”体现在“最后裂项之后,结果是两个分数相减的形式”,这是“裂差”名字的由来)。
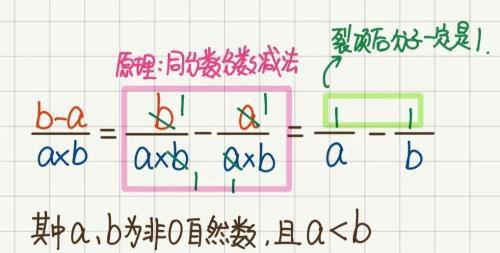
图4
目前为止,有两处知识学生运用时非常容易出错:(1)图4规律的前提条件:母积子差;
(2)结论易错点:符合“母积子差”的分数裂项后,相见减的两个分数分子一定是1!(你知道为什么吗?想一想这个1是怎么得到的?没错!此处1是约分得到的,与a、b分别为多少没有太大关系!
二、分数裂差的运用。
1⃣️分数裂差基础问题剖析:

图5
1解题思路分析:
(1)分析条件:观察计算题,可以从两方面入手,一是数,二是运算符号。首先,观察数,我们发现单个的分数都符合“母积子差”(这是一个重要的突破口,由此我们联想到了今天所学的内容“分数裂差”)。再观察符号,符号都是加号。
(2)过程书写:
第一步:先利用分数裂差的知识,将分数逐一裂项;(书写时,建议前后各裂两个分数,中间用省略号表示,这样做有一个好处,方便第二步观察哪些分数能够抵消掉)
第二步:“消消乐”,需要知道哪些数能够抵消掉,还剩下哪些数。
第三步:计算得出最后结果。
2分数裂项之所以难,是因为它的题型千变万化,如图6至图8所示。

图6
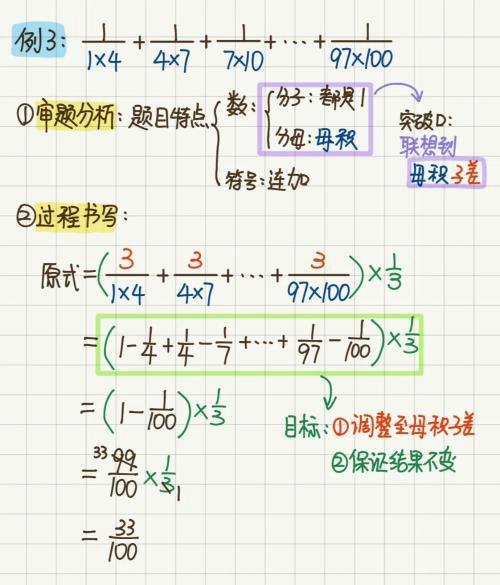
图7

图8
2⃣️分数裂差问题的拓展
仔细观察一下例题5(如图9所示):
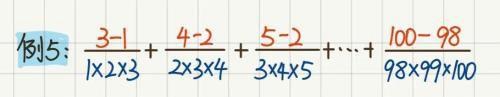
图9
通过题中的数,不难发现,单个分数的分母是三个数的乘积的形式(简称“母积”);单个分数的分子是一头一尾两个数的差的形式(简称“子差”),和我们前面讲解的分数裂差的特点类似,用字母表示如下:
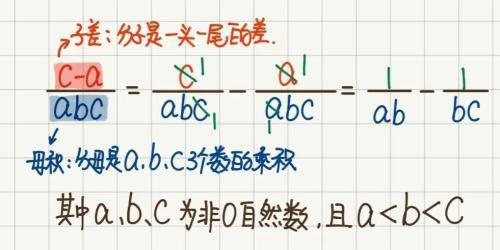
图10
借鉴之前我们所说的同分母分数减法的原理,我们发现图10中这类符合“母积子差”的分数也可以利用同分母分数减法原理裂项变为两个分数相减的形式(如图11所示):
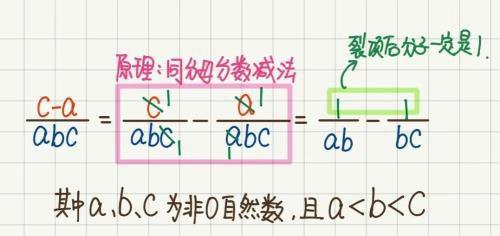
图11
刚开始,对于这个规律的运用,学生可能不太熟悉,可以先让学生尝试用上述规律解决一下此类型的问题,如图12所示:
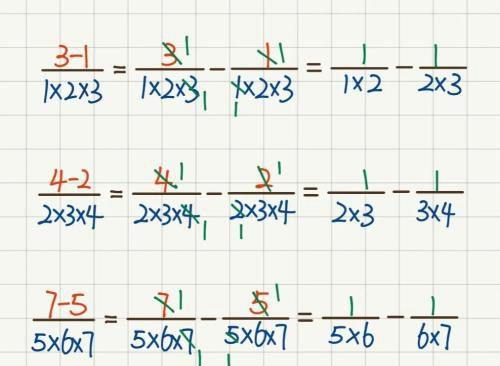
图12
规律掌握熟练后,接下来就是运用的问题啦,回到我们刚刚所说的例题5,我们再来尝试解决一下这题。

图13
1解题思路分析:
(1)分析条件:计算题先从数和符号两方面入手。首先,观察数,我们发现单个的分数都符合“母积子差”(这是一个重要的突破口,由此我们联想到了今天所学的内容“分数裂差”)。再观察符号,符号都是加号。
(2)过程书写:
第一步:先利用分数裂差的知识,将分数逐一裂项;(书写时,建议前后各裂两个分数,中间用省略号表示,这样做有一个好处,方便第二步观察哪些分数能够抵消掉)
第二步:裂项相消
第三步:计算得出最后结果。(要注意:最后结果是整数的要写成整数,是分数的要写成最简分数的形式)
2到这里,相信你对分数裂项有了更进一步的认识,结束本次学习前不妨来挑战一下下面2道题(如图14、15所示):
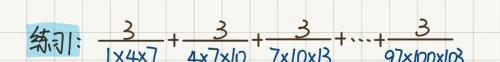
图14
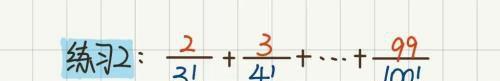
图15
以下是练习1、2的答案详解(如图16、17所示):

图16
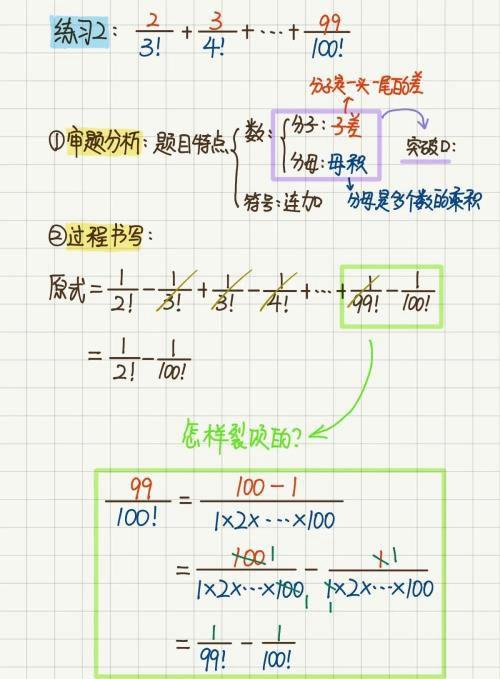
图17
最后,来用一张思维导图来汇总回顾一下本章所讲解的知识(如图18所示),思维导图上还给大家补充了分数裂和的内容,感兴趣可以了解一下。
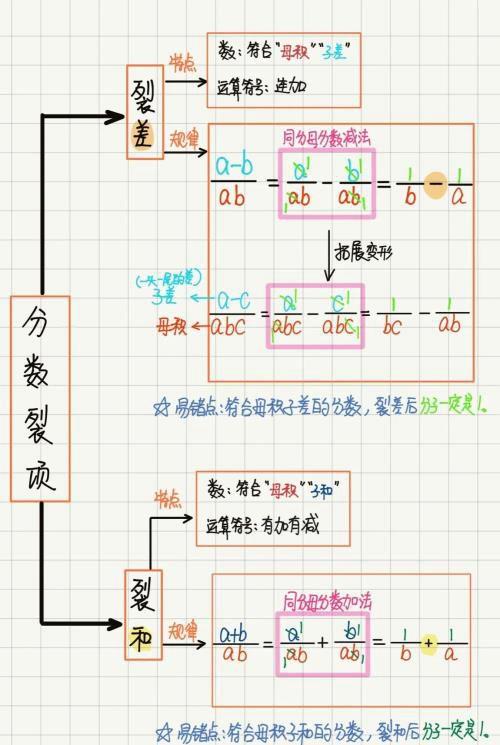
图18
如果这次分享对于你有帮助,别忘记点赞➕收藏哟[送心][玫瑰][机智]
免责声明:本站部份内容由优秀作者和原创用户编辑投稿,本站仅提供存储服务,不拥有所有权,不承担法律责任。若涉嫌侵权/违法的,请与我联系,一经查实立刻删除内容。本文内容由快快网络小玥创作整理编辑!