赋范线性空间例子(赋范线性空间成为baach空间需要范数足)

导语：从三维空间衍生而来的数学空间——赋范线性空间

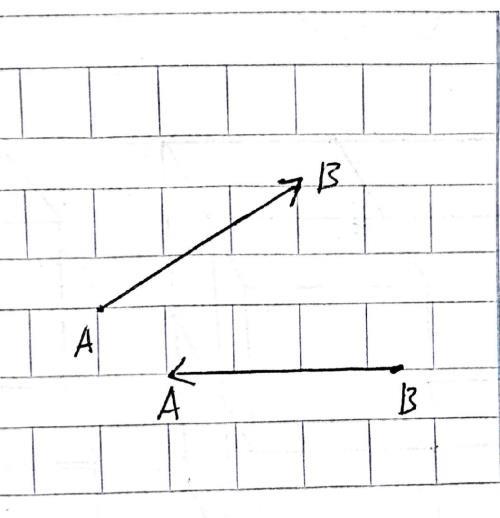
在三维空间中任意取两个点A和B，我们用有方向的线段将A点和B点连接在一起。如果线段的方向是从A到B，那么我们将这个有方向的线段记作向量AB。如果线段的方向是从B到A，那么我们将这个有方向的线段记作向量BA。

我们常见的数量有两种，一种是标量，只有大小，没有方向；另一种是矢量，既有大小，又有方向。显然向量就是矢量，我们把向量的大小称为向量的模长，简称模。向量的模其实就是连接向量首尾两端线段的长度。向量AB的模一般记作|AB|.

根据模长的定义，我们可以知道向量的模具有一下特点：

①非负性：|AB|≥0;

②齐次性：a是任意一个，|aAB|=a|AB|;

③三角不等式：(根据三角形三边长度的关系)

|AB|≤|AC|+|BC|

其中，AB，AC，BC是同一个空间的三个向量.

在数学的世界里不仅仅有几何空间，还有函数、矩阵、多项式等等其它东西组成的空间。在这些空间里，模长依然存在，只不过它不叫模长而叫范数。

范数的定义：

设V是一个线性空间，对于V中任意一个元素x，定义实值函数||x||，||x||满足一下条件：

①非负性：||x||≥0;

②齐次性：a为任意一个数，||ax||=a||x||

③三角不等式：||x+y||≤||x||+||y||,y是V中的元素.

则称||x||为x的范数，V为赋范线性空间。

在几何空间里我们可以用模长来表示空间中元素之间的距离。

例如，向量AB的模长就是点A到点B距离。

在赋范线性空间里，我们也可以用范数来表示空间中元素的距离。

由范数诱导的距离(用范数表示距离)：

设V为赋范线性空间，x,y是V中任意两个向量，定义d(x,y)=||x-y||

满足下列条件：

①d(x-y,0)=d(x,y);

②d(ax,y)=|a|d(x,0),a是任意一个数.

这样x与y之间的距离就是||x-y||.

本文内容由快快网络小娴整理编辑！