瓜豆原理值问题(瓜豆原理初中解法)

导语：中考数学：构造法、瓜豆原理求最值

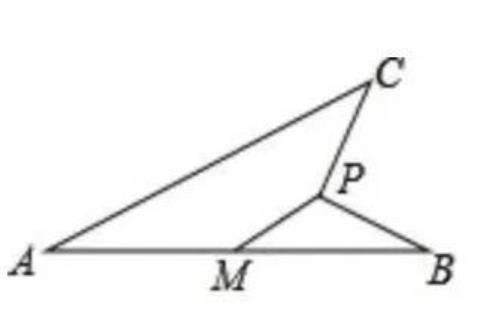
如图，线段AB=4，M为AB中点，动点P到点M的距离是1，连接PB，线段PB绕点P逆时针旋转90°得到线段PC，连接AC，求线段AC长度最大值。

方法一：构造法

分析：连接BC，取BC中点E，连接ME，因为点M为AB中点，所以ME=1/2.AC，以BM为直角边作等腰△BMD，连接PD

∵点E为中点

∴BE/PB=√2/2，又BM/BD=√2/2

∴手拉手易证：△BME～△BDP

∴ME/DP=√2/2

∵DP≤DM+PM=3

∴ME最大值=√2/2.DP=3√2/2

∴AC最大值=2.ME=3√2。

方法二：瓜豆原理

分析：主动点：P，从动点：C，中心点：B

主动点P运动轨迹：是以点M为圆心，以MP长为半径的⊙M上运动。

从动点C:是主动点P，以点B为旋转中心顺时针旋转45°，放大√2倍得到。

∴从动点C：是主动点P对应轨迹顺时针旋转45°，放大√2倍得到。

将BM绕点B顺时针旋转45，°放大√2倍得到BO（圆心也顺时针旋转45°）

∴点C运动轨迹：以O为圆心，OC长为半径的⊙O上运动

∵△BPC，△BMO为等腰Rt△

手拉手模型易证：△BCO～△BPM

∴CO/PM=BO/BM=√2

∴OC=√2.PM=√2

当：点C运动到点A、O、C共线时AC取得最大值

Rt△OAM中:OA=√2.AM=2√2

∴AC=OA+OC=2√2+√2=3√2。

本文内容由快快网络小媛整理编辑！