有限元偏微分方程和边界条件的弱解形式一样吗(偏微分方程及有限元分析)

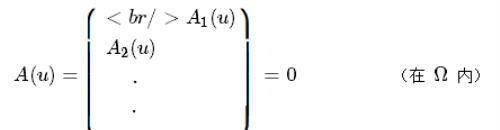
导语：有限元偏微分方程和边界条件的弱解形式

1.什么式弱解？

弱解 (weakformation) 是建立在变分法基础上的，通过这个方法将strong form 的PDE转换为weak form，使得有限元的求解成为可能。

2.为什么要了解弱解？

大部分商软都内置了偏微分方程转换成弱积分形式，不用去理会。但是有时候经典的偏微分方程不能解决实际问题，如基于岩石的粘弹性问题求解，需要考虑诸如maxwell体进行本构重建，而软件又没有该模块时，会考虑用弱形式；另外弱形式的表达方式较偏微分方程更紧凑易懂；三，也可以帮助对有限元的深入了解。四，传统的固体力学采用最小势能原理求解偏微分，但延伸到传热、流体等领域，用最小势能原理已不适用，只能采取弱形式求解。

3.弱解的来龙去脉

由于有限元方法是结构力学家发明的，其基本原理是基于变分法与分片插值多项式两项技术，但是有限元技术的推广与研究的深入使得今天的有限元方法已突破了这两项技术的范围。 例如，为了把有限元方法应用于非结构力学领域，如流体力学领域，人们不得不采用虚位移原理即“弱形式”取代变分原理，为了求解无界区域问题或者奇点问题， 采用非多项式的形函数(基函数)将具有更好的精度，因此形函数不得不突破分片插值多项式的限制。

具体讲，弱解形式的数学表达可以从以下思路获取：

工程或物理中许多问题，通常是以偏微分方程和对应的边界条件的形式提出来的，可以一般地表示为未知函数 u 满足偏微分方程组：

式1

其中 Ω 域可以是体积域、面积域等，如下图所示。同时未知函数u还应满足边界条件：

式2

而要求解的未知函数u，可以是标量场函数(例如温度)，也可以是几个变量组成的向量场函数(例如位移、应变、应力等)。 A、B是表示关于相互独立变量(例如空间坐标、时间坐标等)的两个微分算子。偏微分方程 数目应和未知场数目相对应，因此，上述偏微分方程可以是单个的方程，也可以是方程组。

于工程或物理学中遇到的偏微分方程一般是没有理论解的，即未知函数没有解析表达式。而工程上又需要了解这些未知函数，所以一般用数值方法来求解这些偏微分方程。有限元方法就是一种求解偏微分方程的数值方法，它实际上求解的是偏微分方程的弱解积分形式，所以需要先将偏微分方程变成其弱解积分形式，才能使用有限元方法。

由于偏微分方程在域 Ω 中每一点为零，因此就有

式3

在很多情况下可以对上式进行分部积分得到另一种形式：

式4

其中 C,D,E,F 是微分算子，它们中所包含的未知函数导数的阶数较式3的微分算子 A 低，这样对函数 u 只需要求较低阶的连续性就可以了。式4是偏微分方程组式1的弱解积分形式或“弱”形式， 或称之为虚位移原理。

本文内容由小嫣整理编辑！