光为什么走短的路径(光总是走时间短的路径)

导语：最短的路径

我们知道，光在均匀介质中是直线传播的，也就是说，按最短路径传播。然而，当光不能从一个点直接到达另外一个点，而是要经过镜面反射才能到达的时候，光选择的同样是最短路径。

现在让我们来研究一下光的传播路径。设图101中的字母A表示光源，直线MN表示镜子，而线ABC表示光线从蜡烛到人眼C的传播路径。直线KB垂直于直线MN。

根据光学基本定律，反射角2等于入射角1。知道这一点，就很容易证明，在从A点到C点但必须经过镜面MN的所有可能路径中，路径ABC是最短路径。为此，只需要把路径ABC同任意一条其他路径，比如ADC（图102），做一下比较。我们从A点引出直线MN的垂直线AE，AE的延长线与射线BC的反向延长线相较于F点。用线段连接F点和D点。我们首先证明三角形ABE与三角形EBF全等：两个三角形都是直角三角形，有一个公共的直角边EB，另外，角EFB与角EAB相等，因为它们分别等于角2和角1。所以，AE=EF。两个直角相等，可以推出直角三角形AED与EDF全等，因此，AD与DF相等。

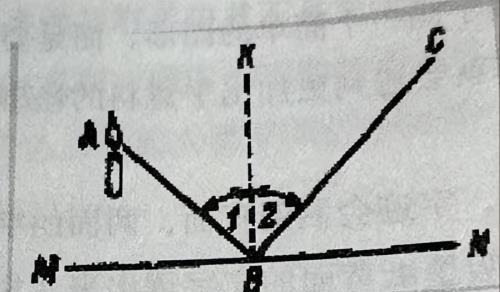
图101 反射角2等于入射角1

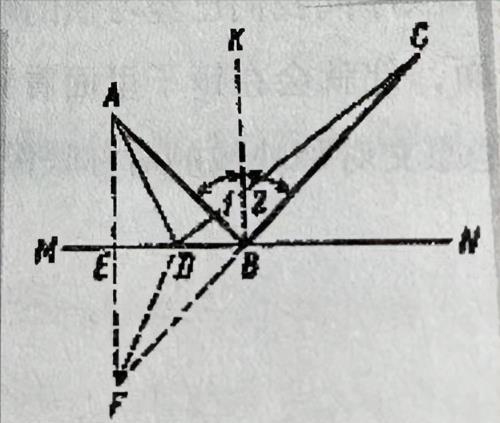
图102 光线反射时沿最短路径传播

因此，我们可以把路径ABC替换为与之相等的路径CBF（因为AB=FB），而把路径ADC替换为CDF。比较线CBF和CDF的长度，我们就会看到，直线CBF要短于折线CDF。因此，路径ABC要短于ADC，而这正是我们需要证明的！

无论C点在什么位置，只要反射角等于入射角，路径ABC就永远短于路径ADC。这就是说，光线在光源、镜子和人眼之间传播时，一定会在所有可能路径中选择最短和最快的路径。最先指出这种情况的，是2世纪著名的希腊机械师和数学家----亚历山大城的希罗。

----摘自《趣味物理学》

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小迪创作整理编辑！