多个自变量对一个因变量的影响程度(多个自变量对一个因变量的影响怎么建立模型)

导语：多个自变量对一个因变量的影响（SPSS：协方差分析）

协方差分析解决的问题：多个自变量（包括离散变量和连续变量）对一个因变量（连续数据）的影响。自变量中的连续变量被作为协变量加以（控制变量）。

协方差分析可以在一定程度上排除非处理因素的影响，从而准确的获得处理因素的影响。

协方差分析的条件：除了满足一般的方差分析条件外，还需要满足。

协方差分析是回归分析和方差分析的结合。

分析步骤包括两个部分：

第一部分：平行性检验

自变量与协变量的交互作用：P＞0.05，满足平行性检验，满足协方差分析的条件；P≤0.05，不满足平行性检验，不满足协方差分析的条件。

第二部分：协方差分析

案例：

运动干预对高血压人群的治疗效果研究

实验设计（简化版）：选取54名高血压人群，随机分为3组，分别采用健身走、广场舞、太极拳运动干预。干预时间为6个月。实验前、实验后测试安静收缩压，差值形成变量。已经统计检验过，实验前三组的收缩压基础值差异没有统计学意义。

统计分析思路说明：考虑到年龄可能对血压下降程度有较大影响，而年龄又是连续变量，因此把作为。在研究运动干预对血压影响的同时，排除协变量的影响，使结果更加准确。协方差分析就是用于解决类似问题的。

自变量：锻炼项目

协变量：年龄

因变量：血压下降。

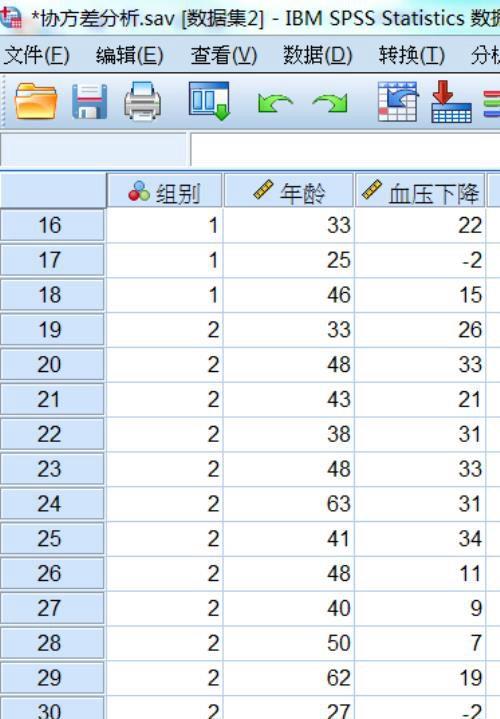
1 部分数据

图1

2 平行性检验

这是协方差分析的一个重要条件。意思是：各组的协变量与因变量存在线性回归关系且斜率基本相同。也就是回归直线近似平行。

可以先做一个散点图，初步探索平行性。

图2 散点图

根据图2，三条回归直线近似平行，可以尝试采用协方差分析。

SPSS步骤：

1）分析-一般线性模型-单变量

图3

2）为；为；为。

图4

3）点击。

图5

4）点击，然后把因子与协变量的主效应和交互作用都选到列表（默认是没有交互作用的）。点击。

5）返回后，点。下面是结果。

图6

组别与年龄的交互作用，P=0.770＞0.05，说明交互作用不显著。也就是满足平行性检验。

因为交互作用不显著，可以精简模型。把交互作用剔除，再做协方差分析。

3 协方差分析

1）图4状态点击，把和的交互作用取消。点击。

图7

2）回到图4后，点击，如下图勾选。点击，返回后，点击查看结果。

图8

4 SPSS结果

1）方差齐性检验结果

图 9

P=0.462＞0.05，方差齐性。满足了协方差分析的另一个条件。

2）方差分析表

图10

组别P=0.019＜0.05，说明三种运动干预方式对血压下降的效果不同。

年龄P=0.000＜0.05，说明年龄的确对血压下降程度产生了影响。排除这部分影响后，使运动干预对血压的影响结果更加准确。

图11

结合图11均值可知。结果：降压效果由高到低依次为HIIT、持续有氧、核心训练。（当然，如果结合后面的成对比较统计结果进一步做出判断会更加合适，篇幅原因，不再展开。）

5 请一定要往下看

如果不考虑这个协变量对因变量（血压下降）的影响，结果会怎样？

1）为；为。其他全默认。直接点击。

图12

2）方差分析表

图13

组别P=0.133＞0.05，说明三种运动干预方式对血压下降的效果相同。

由此可见，不考虑协变量时得出了与前面完全相反的结果。

这提示我们：科学研究中选择准确统计方法的重要性，方法一旦选错，我们将无法追求科学真理。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请反馈，一经查实立刻删除内容。本文内容由快快网络小心创作整理编辑！