角平分线有关的定理(角平分线能得出什么)

导语：冲刺中考36：由角平分线定义推位置，据30°角性质求长度

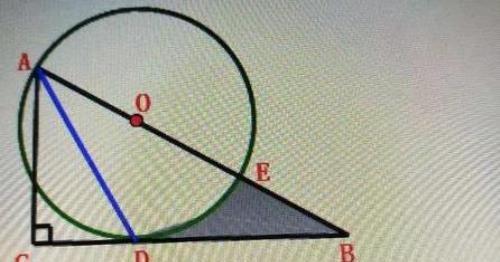
题目：如图1，在Rt△ABC中，∠C=90°，∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O，使⊙O经过点A和点D.

（1）判断直线BC与⊙O的位置关系，并说明理由；

（2）若AC=3，∠B=30°，

①求⊙O的半径；

②设⊙O与AB边的另一个交点为E，求线段BD、BE与劣弧DE所围成的阴影部分的面积（结果保留根号和π）.

图1

解析：(1)直线BC与⊙O相切.理由如下：

如图2，连接OD，则OD=OA，所以∠ODA=∠OAD；因为AD平分∠BAC，所以∠OAD=∠DAC，所以∠ODA=∠DAC，所以OD//AC，因为∠C=90°，所以∠ODB=90°，

所以BC⊥OD，因为BC经过半径OD的外端点D，所以直线BC与⊙O相切.

图2

(2)①在Rt△ABC中，∠C=90°，AC=3，∠B=30°，所以AB=6；

设⊙O的半径为R，则OA=OD=OE=R，因为OD=1/2OB，所以R=1/2(6-R)，所以R=2.

②在Rt△BOD中，∠ODB=90°，OD=2，∠B=30°，所以OB=4，∠BOD=60°，

所以BD²=OB²-OD²，即BD²=4²-2²，所以BD=2√3；

因为阴影部分的面积=Rt△BOD的面积-扇形ODE的面积，

所以，阴影部分的面积为:1/2×2√3×2-60/360×π×2²=2√3-2π/3，

所以，线段BD、BE与劣弧DE所围成的阴影部分的面积是2√3-2π/3.

点拨：

角平分线的定义；内错角相等，两直线平行；在直角三角形中，30°所对的直角边等于斜边的一半；扇形面积计算公式；等是解证此题的基础.

本文内容由小萱整理编辑！