三年级的鸡兔同笼怎么解(小学三年级鸡兔同笼问题解法)
导语:三年级也能学会的“鸡兔同笼”
今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?
意思是:鸡和兔头共35头,腿共94只,问鸡兔各几只?
这道题 “鸡兔同笼”,最早出现在1500多年前的《孙子算经》中。三十多年前,这是初中一年级教学“二元一次方程”时的内容,近几年是苏教版六年级教学“解决问题的策略”时的内容。
这道题在小学阶段,比较难!很多六年级同学都不会做。
今天,我来教你一种三年级同学都能学会的方法。
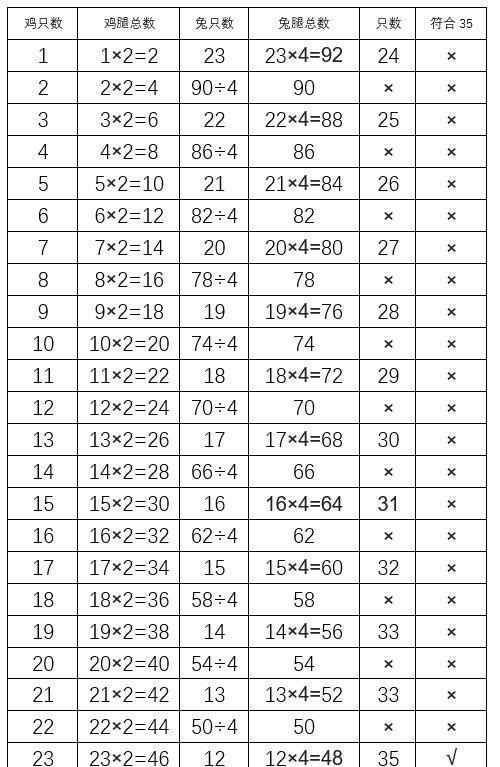
首先假设鸡有1头,那么鸡的腿共有2只,剩下兔腿共92只,兔的只数就是92÷4=23,但1+23=24,24不等于35,错!
假设鸡有2头,那么鸡的腿共有4只,剩下兔腿共90只,90÷4除不尽,错!
假设鸡有3头,那么鸡的腿共有6只,剩下兔腿共88只,88÷4=22,3+22不等于35,错!
……
请看表格:
鸡有23只,兔有12只时,腿共23×2+12×4=94,头共23+12=35,总算做出来了!这个方法只要不偷懒,一个一个的慢慢算,最后肯定能算出来,没有什么懂不懂的吧?
可有些同学说,太多、太烦了,能不能快点?
想偷懒!那接下来认真看吧!
注意看表,刚才的表中,鸡是一次1只慢慢加的,其实你可以一次加2只、3只、甚至一次加10只!看下表:
当你算到鸡有21只时,鸡兔总只数共33只,这时你应该感觉到接近正确答案了吧?从21只开始,再一次加1只,前后一共试了5次,就试出来了吧!
当然,这些数字有可能还得看运气,加的太多有可能跑的太远!那么你还可以从中间试起,35÷2≈18,假设鸡有18只,然后再试,看下表:
6次就试成功了!
在不断调试的过程中,你发现了吗?一次调试腿总数正好,但总只数不符合35。下一次肯定腿总数不正好(除不尽),那还可以跳着试。18不行,19行,20不行(可以不算),21行,22不行(可以不算),23行(成功),一共试了18、19、21、23共4次。
试着做一条: 鸡兔同笼,共有45个头,146只脚。笼中鸡兔各有多少只?
45÷2≈23,从鸡有23只试起。
鸡有23只开始试,不行;鸡有24只,结果总数49只,越来越多,说明鸡的只数不能多了。多加不行,那么就减少鸡的只数。鸡21只,不行;鸡19只,不行;鸡17只,搞定!这回的数字比上一题大多了,也只试了5次就搞定了!
你还可以先试试兔的只数,慢慢试吧!试试、算算、看看、想想,只要不偷懒!没准儿,你能更快点找出正确答案呢?甚至想出更好的方法算出鸡兔各多少只呢?
本文内容由快快网络小婷整理编辑!