数学方阵中包含的数学原理是什么(数学方阵中包含的数学原理是)

导语：数学方阵中包含的数学原理

前一篇《没有任何数字的证明：用队列方阵证明根号2是无理数》中我们用方阵巧妙的证明了根号2是无理数，方法简单巧妙，展现了数学无穷的魅力，两个相同数的平方和永远不可能等于一个平方数。

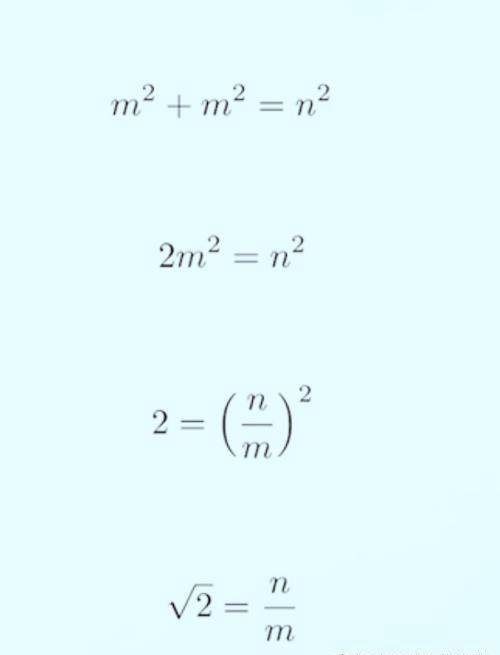
那么对于相同方阵（即两个相同数的平方）可以写成如下差一点点的例子，12平方加12平方等于17平方减1，只是用这个来演示一下

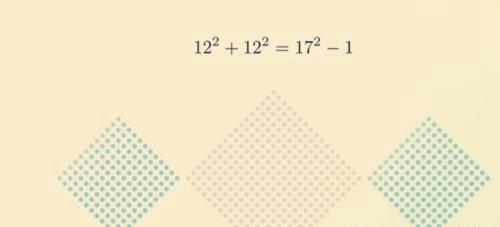
我们现在以一个不错的对称形式再做一遍，这会有个不错的发现，大家可以一起看下，就这样汇聚这两个方阵，然后我们像之前一样有重叠部分

然而因为我们其实是用相差1的例子，如果是完全相等的，那么绿色部分应该和灰色这两个区域是相等的，但是我们其实相差1，所以这次也应该是相差1，如果不相信，你可以数一下

这是另一个只相差1的例子，我们继续，去除蓝色部分，剩下

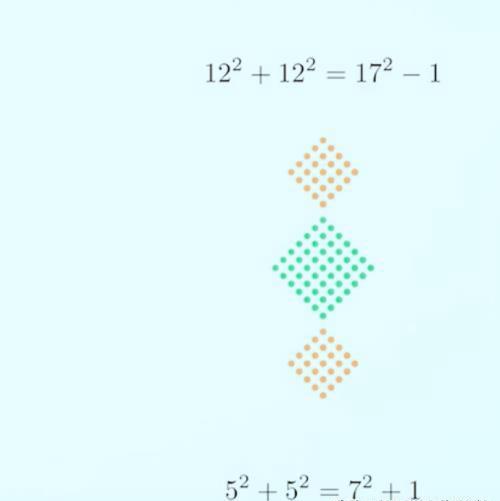
我们再把这两个家伙汇聚到当中，他们也会有重叠部分

让我们看看这里是多少，我们有2的平方，然后有两个方阵，那就是8，离9 差1

所以这又只相差了1

还有吗？我们还能继续下去吗？，这个特别简单，但又是只相差了1，1的平方加1的的平方等于1平方加1

有了一个“只相差1”，我们就得出了其他所有的，只要重复这个汇聚的过程，还挺有趣的，而且我们得到的都是越来越小的，但我们也能倒着来，如果我们从这里往回倒的话，我们就能得到全体“只相差1”，让我们往回倒吧

分离

然后补上方阵

同理：分离然后我么再补上方阵

继续延伸，我们就回到《没有任何数字的证明：用队列方阵证明根号2是无理数》中的方阵

如果我们想要下一个更高次的，我们只要补上一个大正方形在周围，如果你再拿这两个方阵排列一下

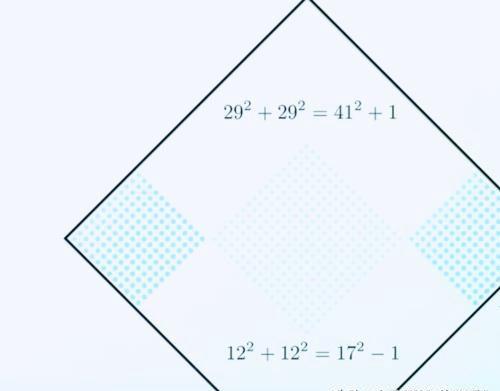
补上一个大方阵，我们就得到一个接一个的等式，实际上我们得出了所有满足：两倍平方和等于平方和加减1的等式

这是我们得出的4个例子，这些“只相差1”，他们的其他形式也挺不错的，如下左边其实是1和1,3和2,7和5

如果你把他们看成分数，继续，然后你觉得会发生什么？它们越来越接近根号2

人们对π的认识中有一个就是22/7约等于π的值，如果你想找一个分数可以接近根号2，大概会用17/12, 17/12对根号2，就像22/7对于π

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小林创作整理编辑！