大学学平面几何吗(大学数学几何学学什么)

导语：进入大学前先要掌握的数学-平面几何

一、三角形

定义：由不在同一条直线上的三条线段首尾顺次相接组成的图形。

等边三角形（正三角形）：三条边都相等

等腰三角形：两条线段相等。

等腰三角形是轴对称图形，底边上的高、中线、顶角的角平分线重合（三线合一）

性质：两边之和大于第三边，两边之差小于第三边。

垂心：三条高交于一点，重心分中线成2:1的两部分。

内心：三条角平分线交于一点。

内切圆：以内心为圆心，内心到各边的距离为半径。

外心：三条垂直平分线交于一点。

外接圆：以外心为圆心，外心到各顶点的距离为半径。

二、四边形

定义：又不在同一直线上的四条线段首尾顺次相接组成的图形。

平行四边形：两组对边平行。

矩形：一个角为直角的平行四边形。

菱形：一组邻边相等的平行四边形。

梯形：一组对边相等，另一组对边不平行的四边形。

三、圆

不同直线上的三个点确定一个圆。

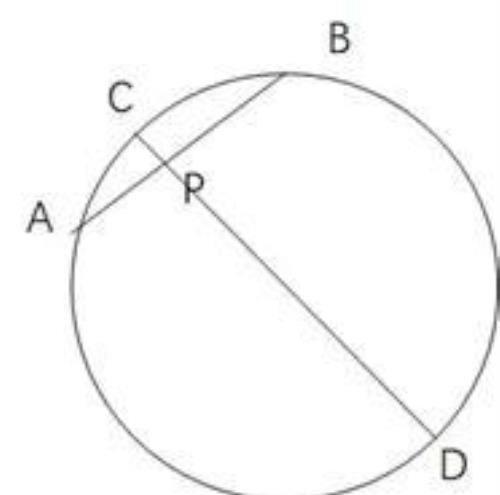
过圆一点P作圆的两条弦AB，CD。则点P内分AB，CD所成四线段有数量关系：

AB·BP=CP·DP

过圆外一点P作圆的两条割线PAB，PCD，则点P外分AB，CD所成四线段有数量关系：

AP·BP=CP·DP

垂径定理：在圆O中，半径OH与弦AB相交于点C，且点C是AB中点，则OC⊥AB。

在凸四边形中，若对角互补，则四边形四顶点共圆。

在凸四边形中，若一个外角等于它的内对角，则四个顶点共圆。

同底的两个三角形，若两顶点都在底的同旁且顶角相等，则两个三角形的四个顶点共圆。

一、相似形

射影定理：在直角三角形RtΔABC中，∠C为直角，CD⊥AB于D点。则有：

CD2=AD·DB AC2=AD·AB BC2=BD·BA

本文内容由小海整理编辑！