矩阵的性质和运算法则(矩阵性质公式大全)

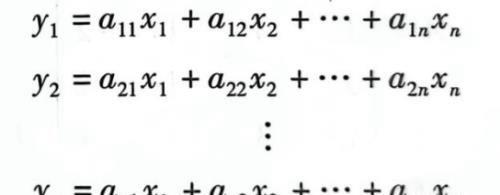
导语：一篇文章搞定矩阵——第二篇 矩阵的性质以及抽象，特殊矩阵

一篇文章搞定矩阵

——第二篇 矩阵的性质以及抽象，特殊矩阵

大家都知道矩阵这一块呢，题目中条件的出现很多都是符号语言。那么从条件到问题之间的双向奔赴，就需要我们掌握每一个“符号”所牵涉到的各种性质，下面就来详细的罗列和解读矩阵所涉及到的性质。

前面说过，矩阵就是一个数表，作为数，那么就自然会有运算。矩阵的求和与求积运算是这里最常见的运算（加减，乘除互为逆运算）。

一，矩阵的加法与数乘

先来分析矩阵的加法，两个矩阵相加，这就要求二者必须是相同排列（形状）的，不然的话会有元素多余或者漏下。深层次来解释原因如下：

两个矩阵相加的结果实际上是两个矩阵所代表的两个线性集合组相加后得到的新线性集合组的系数（线性集合组如下图）。如果两个线性集合组x,y的个数，排布不相同的话，肯定是无法相加减。（矩阵的元素均为x系数而出现的），也可以看出：矩阵的加减的结果就是每一个对应的元素直接相加减后所得的结果。 按照这个思想，我们不难发现矩阵的数乘也很好分析，就是在集合组系数上同时乘以常数，就可以得到一个新的线性集合组，所以说数乘也是比较符合我们常规的认知的。

一言以蔽之，矩阵的加减就相当于数字的加减，矩阵的数乘就相当于数字的乘法，满足交换，结合，分配三个定律。转化为符号语言就是:A+B=B+A, k（A+B）=kA+kB

二，矩阵的乘法

首先说明，矩阵的乘法是抽象出来的一种运算，并不是真的有两个线性集合组相乘。就像是一种新定义问题：记图一系数数表为矩阵A，图二系数数表为B，A乘以B的含义被赋予为，把B所代表的线性集合组代入到A所代表的中去，这也就解释了为什么矩阵的乘法不具有交换律的原因，把A式代入到B式中当然和把B式代入到A式中不同。

然后我们来分析以下代入所需要的条

件，首先必须得保证左边有P个y项，右边也有p个y项吧，这是很显而易见的，那么对应起来就是A中的列数等于B中的行数。而矩阵相乘所得到的结果是x对于z的线性集合组的系数。不难看出，最终的矩阵继承了前式的行数和后式的列数。而在表面上我们看到的就知识以下的乘法法则：

如此看来，矩阵的乘法就不能满足交换律了，只能满足鸡肋的结合律和分配律。如下图：

。

三，混合运算

这一块算是解题最实用的性质了，利用表中的性质，我们可以放心的来代换，巧解题目。此处将性质悉心归纳，整理成表格（还不赶紧三连！！！）

大家可以看到，这里有很多的不一定存在，但是不要不敢去操作，只要我们掌握的够多，见的世面够广，考试题就都是老朋友。下面来介绍几个经典的条件与结论：

四，矩阵的秩

求矩阵的秩是一个常见和基础的问题，一般有三种方法：分别是1.化阶梯型法2.极大无关组法3.分块阵初等变换法。这里只着重讲一三种解法。

第一种，顾名思义，就是把原矩阵化成阶梯型矩阵，如下图所示：

和行化上三角行列式步骤相似，都是用第一行第一个数消去下方正对的所有数，接着第二行第二个数...直至最后一行，最终化成一个阶梯型的矩阵，就可以得出结果。

第三种，利用分块阵的初等变换求秩

说起分块矩阵，实际上它和矩阵在运算上区别不大运算法则也相同，只不过求转置的时候记得把每一个小矩阵在转置一下就可以了。而利用它来求秩，更多的是用不等式夹逼出来的，如下图：

考试的题型留到下一篇文章里讲，下面介绍一下求矩阵的逆矩阵的两种方法：

五，矩阵的逆

（一），初等行变换求逆矩阵

步骤非常简单，只需要在原矩阵右边加上一个单位阵，而后把第二行乘以一个负的D分之B再加到第一行上去就能消去B，用同样的方法也 可以消去C，最后每行同时除以常数使其变为E即可。

（二），分块阵求逆矩阵

这个应用范围变小了，但是更简便了。它需要矩阵的一块为零，然后分割成为分块阵，然后直接套公式即可：

那本篇文章到这里就结束了，矩阵这一块比较重要，大家也能看到文章一篇比一篇长，总结比较费时间，还望各位老板海涵。不过总结出来的绝对是妥妥的精华，下一篇将对矩阵下最后的宣战书，详细的列举矩阵这一块的题型，解题方法。

原创不易，还请多多鼓励。thanks

本文内容由小曲整理编辑！