导语：函数的连续性与间断点

连续性

理解：相当于一条平滑的曲线，不存在间断。

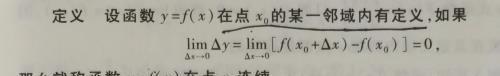
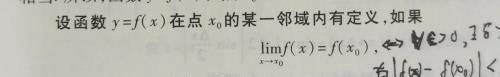
如连续的图像

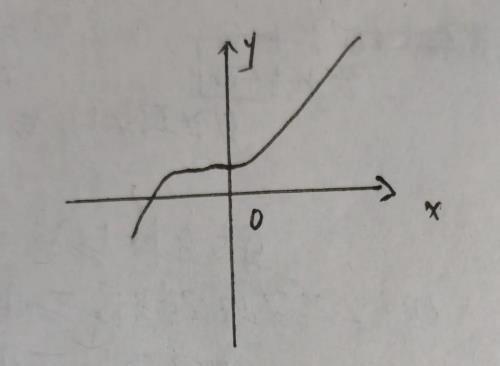
连续性需要注意连续的函数不一定能够求导。

如：

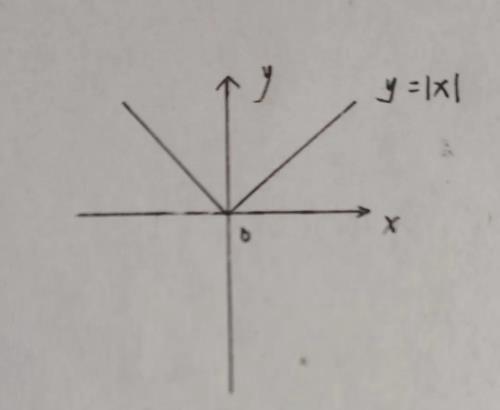
该函数在x=0的时候左导的值（-1）不等于右导的值（1），所以在x=0时不存在导数，但该函数连续。

间断点

设函数f(x)在x0的某去心领域内有定义，在满足下面三种情形之一的都是间断点：

（1）在x=x0处没有定义。

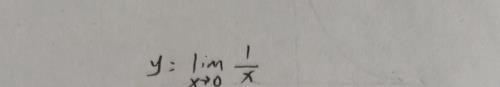
在该函数中x=0没有定义

（2）虽在x0处有定义，但极限不存在。（在分段函数中比较常见）

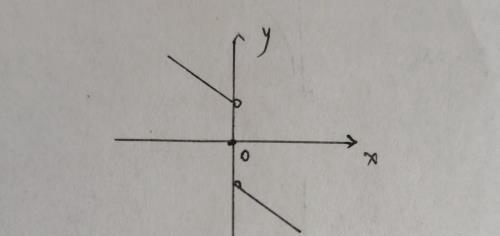
（3）在x0处有定义，但是极限的值不等于函数值。（在分段函数中比较常见）

如图：函数值为0，极限取值为1。

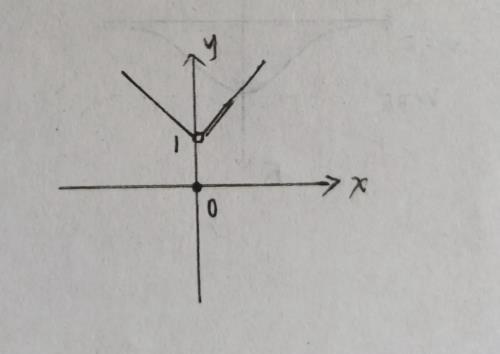
间断点好理解，就是有间断的点，不是连续的点呗。

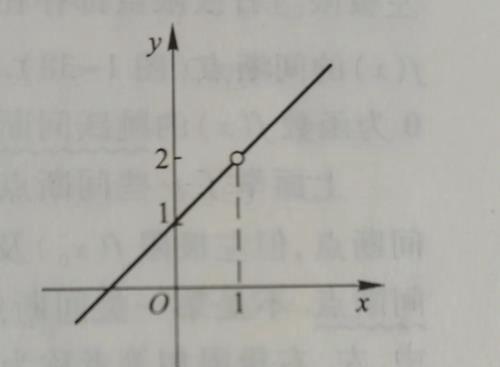
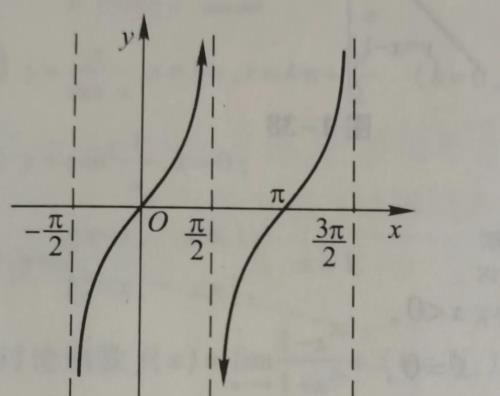
间断点又分为可去间断点和跳跃间断点。

第一类间断点：左极限和右极限都存在。

（1）可去间断点：左、右极限相等。

（2）跳跃间断点：左右极限不相等，图形产生跳跃的现象。

第二类间断点：无穷间断点和振荡间断点。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小岑创作整理编辑！