地球的万有引力重力向心力和惯性离心力的区别(地球引力重力和向心力)

导语：地球的万有引力、重力、向心力和惯性离心力

什么是地球的万有引力、重力、向心力和惯性离心力？它们之间有什么样的关系？下面谈谈个人的粗浅认识。

地球的万有引力

万有引力（简称引力）是在宇宙大爆炸之初最早出现的 、自然界中仅有的四种基本相互作用之一。在探讨的这四个力中，万有引力是基本的自然力，而其余三个力应该是它的“衍生的力”。

1687年，牛顿发表了他的著名的万有引力定律：自然界中任何两个质点都相互吸引，其引力的大小和它们的质量的乘积成正比，和它们的距离的平方成反比。其计算公式

（万有引力定律） （1-1）

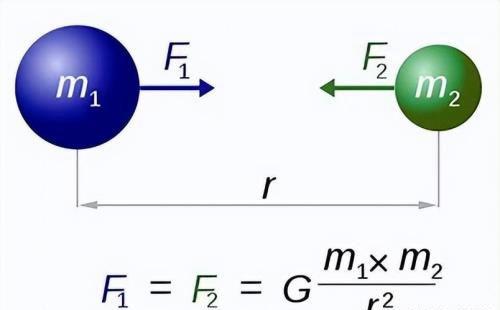
两个质点之间的万有引力满足牛顿第三定律，它们大小相等方向相反，作用在两个质点的连线上。用矢量表示：FF，如图1所示。

图1.万有引力是任何两个质点之间的相互引力

根据牛顿万有引力定律，地球对其表面附近的任何物体都具有吸引力，其公式为

（地球对地面物体的引力） （1-2）

式中是万有引力常数，和分别是地球质量和地面物体的质量，R是地球半径；式中负号表示引力方向与矢径的方向相反而指向地心，见图2。

图2 地球的引力、重力和向心力示意图

地球的重力

地球的重力是地球表面附近的物体由于地球吸引而受到的力。重力表达式为

（重力公式） （2-1）

式中是地面物体的质量，是重力加速度（在重力学中被定义为重力场强度），负号表示重力方向竖直向下。

地球的重力主要是由引力提供的，见图2。在地球表面，重力加速度因不同的位置而不同，其大小随纬度的增加而增大，在两极可达最大（g值大约为9.83)，在赤道最小（g值大约为9.78)。

在地面上的相同地点，g值一般不会变化，但是随着高度的增加会减小。

重力的方向竖直向下。

地球的向心力

地球一刻不停地围绕自身的旋转轴（地轴）转动。随着地球的自转，地球表面的物体会受到向心力的作用，产生向心加速度围绕地轴做近似的匀速圆周运动。其向心力也来自引力，见图2。

质量为m的物体其围绕地轴转动的向心力为

有最大负值；在两极，和惯性离心力的矢量合成图。

为了看清楚这几个力的关系，向心力和惯性离心力放大了许多倍，实则很小。而引力和重力实则很大，重力和引力大小比较接近。

方法一，直接使用矢量合成法则

从图2看到，相对于地心参考系，引力矢量可以分解成重力矢量和向心力矢量，其矢量关系式为

FGF&39;分别是引力矢量、重力矢量和向心力矢量。

从矢量关系式（5-1）可以看出，

在两极，向心力等于零，重力等于引力（,)，此时重力有最大值（9.83m/)，方向指向地心。

在赤道，引力、重力和向心力作用在同一条直线上；向心力有最大负值，重力有最小值（9.78)，方向指向地心。

在赤道和两极之间（），随着纬度的增加，向心力逐渐减小（负值），重力逐渐增大，但仍小于引力（），重力加速度g值在 9.789.83。方向指向地心附近。

方法二，引入惯性离心力

在研究上述几个力的关系时，既要利用地心参考系，又要利用牛顿定律，而牛顿定律只能在惯性参考系中成立。对于地心参考系，由于地球自转的影响，从一定意义上说地心参考系不是惯性系，牛顿定律不能成立。但是如果要在地心参考系为了计算方便继续使用牛顿定律，必须引入惯性离心力的概念。

引入惯性离心力后，图3中的引力矢量F、重力矢量G和惯性离心力矢量C有如下关系:

GFC （5-2）

利用矢量关系式（5-2）分析，在两极，离心力等于零，重力等于引力（,），重力有最大值（9.83)，方向指向地心。

在赤道，引力、重力和离心力作用在同一条直线上；离心力有最大值，重力有最小值（9.780)，重力小于引力，方向指向地心。

在赤道和两极之间（），随着纬度的增加，离心力逐渐减小，重力逐渐增大，但仍然小于引力（），即 9.789.83。方向指向地心附近。

上述两种方法殊途同归，结果一致，这绝不是偶然的。假想的惯性力和实际的向心力大小相等方向相反，作用在相同的物体上，各自和引力、重力构成矢量平行四边形，从而获得相同的结果。但是从牛顿力学角度，似乎方法二更加符合物理上的逻辑。

惯性离心力和向心力的关系

虽然惯性离心力和向心力公式在形式上只差个符号，但是因为惯性离心力就是为了使牛顿定律在非惯性系——地球转动参考系中在形式上也能成立而虚拟的惯性力，实际上并不存在；向心力则是真实存在的力。因此它们既不能构成一对平衡力，也不能构成为一对作用力和反作用力。但是两者关系密切又如影随形，没有转动系统的向心力就不能虚拟出转动系统的离心力。

本文内容由快快网络小快整理编辑！