判断二叉树是否为平衡二叉树算法(判断二叉树是否为平衡二叉树算法数据结构)

导语：判断二叉树是否为平衡二叉树

今天来学习一下，给定一颗二叉树，如何判断这个二叉树是否为平衡二叉树。

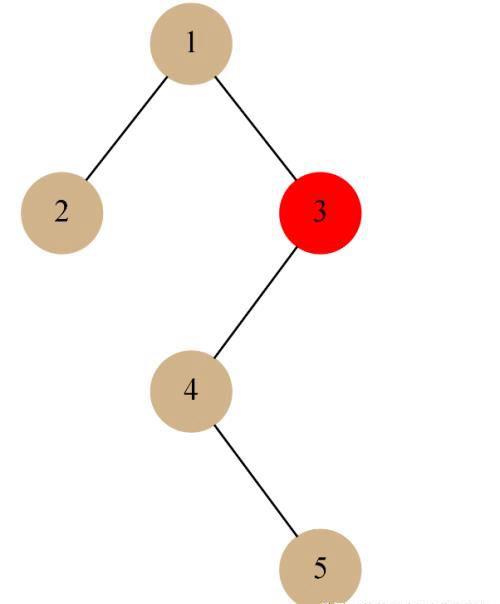
不平衡二叉树

给出如上二叉树，它是不平衡的，输出 false。

判断一颗二叉树是否平衡，就要看它的所有节点是否平衡；而判断一个节点是否平衡就是要判断它的平衡因子（PF）是否小于等于1。与前边学过的ALV（平衡二叉树）不平衡二叉树的旋转（LL、RR、LR、RL） 不同的地方是，现在我们的二叉树节点TreeNode中不包含表示高度的成员。有了高度这个成员是可以直接判断是否平衡的。

现在的二叉树的TreeNode如下：

二叉树的节点

所以这个问题，最直观的想法就是，写一个求高度的函数。求高度函数可以使用递归法，树的高度等于左右子树的高度的最大值再加1，加1的原因是自身节点本身的高度为1。递归二叉树的高度代码如下：

计算二叉树节点高度

有了节点高度之后，我们先看一下普通的解决思路：

判断根结点是否为二叉平衡树（求出左右子树的高度，判断它们的高度差是否超过了1）。递归判断根的左子树是否为平衡二叉树递归判断根的右子树是否为平衡二叉树

这里需要说明的是，空树也是平衡二叉树。

bool IsBlanced_selector(BTreeNode pRoot) {if(!pRoot)return true;//空树也是平衡二叉树    //计算根节点高度差，求出左右子树的高度    int pf = getTheHigh(pRoot->_left) - getTheHigh(pRoot->_right);               if(pf >= -1 && pf <= 1)  //高度差绝对值小于1，再看它的左右子树是否为二叉平衡树       //递归其左右子树        return IsBlanced_selector(pRoot->_left) && IsBlanced_selector(pRoot->_right);             return false;   //高度差绝对值大于1，不是二叉平衡树}

这种方法类似于二叉树的先序遍历，先序遍历了根节点的PF，再先序遍历左右子树的PF。这样的代码效率很低，存在着重复计算。从1开始求高度时，需要遍历3,4,5；到3后，求高度时，还需要遍历4,5；这就导致了重复计算。

既然这样，我们换成后续遍历不就可以了吗？

首先，判断它的左子树是否为平衡二叉树然后在判断它的右子树是否为平衡二叉树判断它们是否为平衡二叉树的同时，记录它们的左右子树的深度最后在判断以这个结点为根的树是否为平衡二叉树

//判断树是否为平衡二叉树(true:是 false:不是)//优化版本(不用遍历重复的结点)bool IsBlancedTree_op_selector(BTreeNode pRoot, int & pdepth){    if (pRoot == NULL)    {        pdepth = 0;        return true;    }    //按照后序遍历去判断,先判断左右子树，然后记录以当前结点为根树的深度    int left, right = 0;//记录左节点和右节点深度//采取传引用的方式，下层递归进行对深度修改以后会影响上一层    if (IsBlancedTree_op_selector(pRoot->_left, left) && IsBlancedTree_op_selector(pRoot->_right, right))    {        int pf = right - left;//计算平衡因子        if (pf <= 1 && pf >= -1)//判断平衡因子是否合法        {//合法就让自身加上子树的深度，然后因为是传引用，所以当递归回到上一层的时候，上层中的right和left就是左右子树的深度            pdepth = left>right ? left + 1 : right + 1;            return true;        }    }    return false;}

这种方法计算下来，只对这棵树进行了一遍后序遍历，时间复杂度会大大下降。

本文内容由快快网络小姬整理编辑！