中考试题垂直的证明思路你能想到多少种题型(垂直证明方法总结)

导语：中考试题，垂直的证明思路，你能想到多少种？

今天这篇文章，我么们继续讨论另一种位置的证法——垂直的证法！中考试题，无论是填空、选择，还是大题都会永达。

我先把自己的思考总结出来，然后用例题进一步解释。

1.基本思路

(1)直接用来断定二线垂直的定理,经常用到的有

(i)等腰Δ顶角平分线垂直底边 等腰底边的中线垂直底边.

(i)勾股定理之理

(i)半圆所对的圆周角是直角

(iv)二圆连心线垂直于公共弦

(v)内、外角的平分线互相垂直

(2)转化、过渡

垂真有时也可转化成等角关系:互补的二角相等 与已知的直角相等

因此,在证的过程中,又常以全等形、相似形为过渡的手段。

(3)计算

我们来看一道经典例题：在圆内接四边形ABCD中,设AB、CD交于E,BC

AD交于F,∠E、∠F的平分线交于G,如图一。

求证：EG⊥FG。

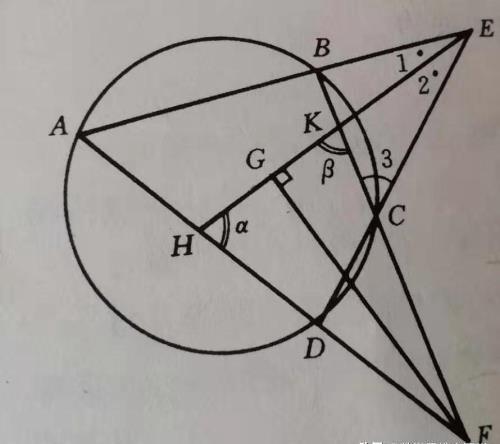
图一

分析：这是一个广为采用的典型之例,条件中有角的平分线,，就有可能利用等腰三角形,共圆的条件又给我们等角转化,或用弧度表角的便利,故有多种证法,现择其三介绍于下:

证法1;利用等腰三角形

设EG分别交AD、BC于H、K,则有

已知:∠1=∠2

共圆:∠A=∠3

∴∠1+∠A=∠2+∠3

又 外角定理a=∠1+∠A，β=∠2+∠3

∴α=β

∴ △FHK等腰

又 FG平分∠F

∴FG⊥HK

即FG⊥EG.

证法2：用狐计算邻补角.

延长EG交圆于M, N,再延长FG交圆于P.Q,如图二，则有

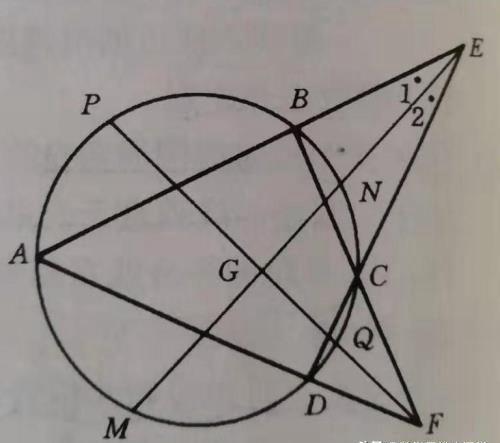
图二

已知: ∠1=∠2 => ½(弧AM - 弧BN) =½(弧MD-弧NC)

所以

弧AM+ 弧CN=弧MD + 弧BN 同理 弧AP+弧 CQ=弧BP+弧DQ

∴ 弧MP+ 弧NQ=弧NP + 弧MQ

=> ∠EGF=∠EGP （互为邻补角）

=> EGLFG.

证法3计算角度

连EF,角的符号如图三所示,这时,只需对△EFG计算顶点E、F处的二角之和,

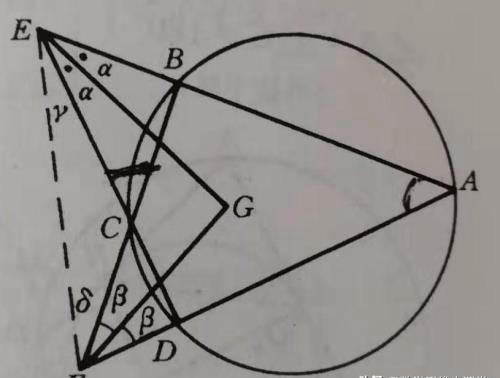
图三

为此,首先,在△AEF中有∠A+2a+2β+γ+δ=180°

再就△CEF,由外角定理知

γ+δ=∠BCE=∠A(共圆)

代入前式,化简即得

(a+γ)+(β+δ)=90°，

∴∠EGF=90°

注:亦可就△BEF和△DEF分别运用外角定理,再由∠ABC、∠ADC互补即可证出。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小岑创作整理编辑！