导语：建筑设计中，应力集中是否会导致结构断裂？

应力集中这个问题，结构工程师大致都清楚，但似乎又不够关注。

本人最近在计算一个钢结构异型截面杆件支座受力的时候，就有这种感觉。如果按杆单元来计算，杆件应力比很小，杆件壁厚甚至可以优化。但如果按实体单元来计算，支座附件由于应力集中，有限元单元应力很大，反而需要局部加厚。

大多数情况下，我们广泛使用杆单元来做结构设计，在支座或节点位置，应力集中是观察不到的。如果专门做节点分析，可以观察到应力集中，但有时我们又会刻意忽略应力集中，只关注平均应力。

● 在结构工程中，应力集中难道不是客观存在吗？为何可以被忽略？

或者，忽略了应力集中，对结构安全的影响是否可控？

难道我们不担心，结构会在应力集中部位逐渐被撕开，从而一点一点地形成断裂面，并最终导致整体结构的破坏？

类似案例并非没有发生过。

最简单的例子，我们用针尖去刺充满气体的气球，应力集中会让弹性十足的气球像玻璃一样发生脆性破坏。

或者，在日常生活中，为了撕开一个塑料袋（零食包装袋）或一块布，我们通常先剪开一个口子，刻意制造应力集中。

高速运行的航天器、飞机、轮船，一个不起眼的结构缺陷，可能会带来魂灭性的灾难。

在过往的结构设计中，为了保证结构安全，结构工程师通常会引入安全系数(2.0以上，重要结构可能达到4.0以上)，确保结构的计算应力远远小于材料强度，这样的设计方法似乎非常保守安全。

但在实际结构中的某些未知区域，真实的应力肯定会比计算应力大得多，比如某些应力集中的部位。此时，所谓的安全系数也显得捉襟见肘，甚至不值一提。

根据简单地代数运算，英格利斯说，若我们有一块材料受到远场应力s的作用，我们在其上制造一个任意形状、长度或深度为L、尖端半径为r的沟槽、裂缝或凹陷，它的尖端及其相邻处的应力为：

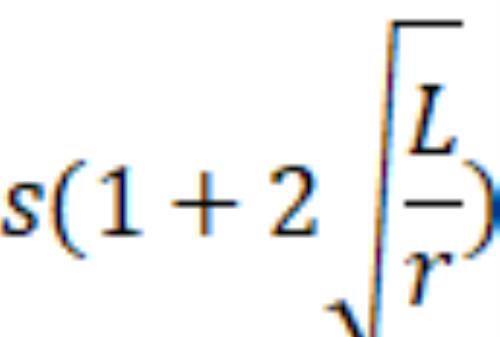
(注：L是裂缝从材料表面向内延伸的长度，如果裂缝在材料内部，则取其长度的一半。)

因此，对半圆沟槽或圆孔洞而言（r=L），其应力值为3s；但对一些尖锐边角的开口来说，r会很小而L会很大，所以边角处的应力可能非常大。

先说圆孔，我们通常会在结构板件上开一些圆孔，比如钢结构采用螺栓连接时的螺栓孔；而对一些焊缝连接，在焊缝的起始部位，裂缝（可能是疲劳引起或焊接缺陷）也会导致较大的应力集中。

如果考虑各种材料缺陷、施工及加工工艺问题、实际使用因素等，应力集中将无处不在。一个负责、认真的结构工程师，仔细面对并思考这些应力集中，看起来应该是理所当然的。

但试图通过安全系数来解决应力集中的问题，这可能会把结构设计推入一个万劫不复的境地，因为我们压根设计不出一个可以承受拉力的、理论上足够安全的结构。

但事实上，在拉伸状态下实际使用的材料，如金属、木材、绳索、玻璃纤维等，都很坚韧。这意味着，它们或多或少会具备某中精妙的机制来抵御应力集中效应。

● 结构断裂究竟是由什么因素引起的？是应力吗？

抗拉强度对应的就是应力的概念。但断裂对应的是能量的概念，体现的是破坏给定材料截面所需的能量值，通常也叫做断裂功。

想想看，一个固体被拉断，意味着至少扩展出一条裂缝且正好贯穿材料并将其一分为二，这样会创造出两个在断裂前并不存在的新表面，为了将材料撕开并生成新表面，需要破坏此前将两个表面结合在一起的全部化学键，这些化学键中蕴含的能量，即等于断裂功。

下面这张表格对比了一些常见固体的抗拉强度和断裂功。

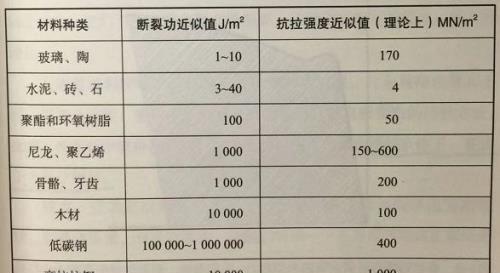
以玻璃和木材做对比，玻璃的抗拉强度是木材的1.7倍，但断裂功仅为木材的1/1000；所以，虽然玻璃的抗拉强度更高，但它比木材脆得多。通常，我们讲，某些材料是脆性的，其实不是说它们的抗拉强度很低，而是指它们被破坏时仅需要较小的能量。

脆性材料和韧性材料，断裂功相差巨大，其本质原因是什么呢？

对我们所关心的大部分结构性固体，破坏任一截面所有化学键所需的总能量大同小异。脆性材料和韧性材料的本质区别在于，破坏过程中所涉及的化学键的数量相差巨大。

脆性固体在断裂过程中所做的功，实质上仅出于破坏新断面或相邻区化学键的需要。

而对韧性材料来说，在断裂过程中，扰动会波及材料精细结构的极深处。

事实上，扰动的深度可达1厘米以上，即可见断面下约5000万个原子的深度。即使只有1/50的原子间化学键在扰动中被破坏，那么断裂功——产生新断面所需的能量——会增加到百万倍。材料内部深处的分子即是以这种方式吸收能量，并在抵抗断裂的过程中发挥作用。

想想软金属的延展性及低碳钢在轴拉力作用下的颈缩现象吧。

● 应力集中是否会引起结构断裂？

我们不得不承认这样一个事实：应力集中在结构中普遍存在，但因此而造成结构断裂却并非那么常见。

很早以前，格里菲斯就研究过这个问题。

假设有一块弹性材料，拉伸后夹住它的两端，使其暂时没有机械能输入或输出，这样，我们得到了一个包含大量应变能的封闭系统。

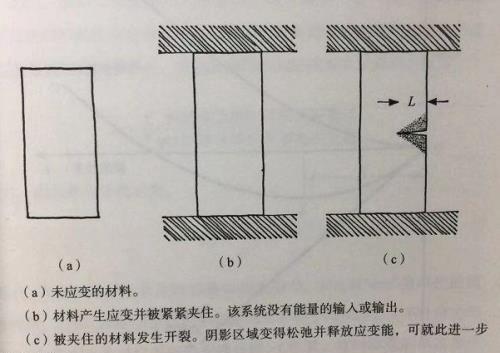
如果我们在材料边缘制造一个长度为L的裂缝，那裂缝是会保持原状，还是会持续扩展，直到形成一条通缝呢？

我们来分析这个问题。

裂缝延长，意味着需要额外的能量供给，因为我们处理的是一个封闭系统，所以能量只能来源于裂缝部位应变能的释放。

格里菲斯的理论认为：裂缝的能量需求随L的增加而增加；而能量释放则随L^2的增加而增加。

所以，存在一个临界裂缝长度Lg，小于Lg的裂缝长度是安全稳定的，且一般不会扩展；而比Lg长的裂缝则会自我扩展，非常危险。

因此，即使裂缝尖端的局部应力非常高，远高于材料的抗拉强度，该结构仍然是安全的，只要没有长于临界长度Lg，它就不会断裂。

这听起来很复杂，但幸运的是，Lg的计算公式非常简单。

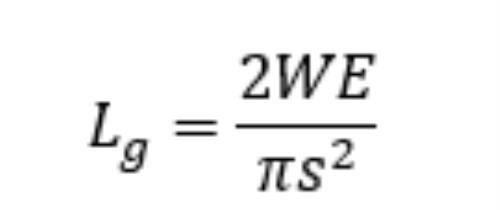
其中，W是以J/m2为单位的裂缝表面断裂功，E是以N/m2为单位的弹性模量，s是以N/m2为单位的裂缝附近材料的平均拉应力（不计应力集中），Lg是以m为单位的临界裂缝长度。

因此，如果想在相当大的应力下安全地容纳一条长裂缝，那么在刚度良好（高E）的材料中，我们需要尽可能大的断裂功W。低碳钢因为兼具良好的断裂功和较高的刚度，而且比较廉价，所以获得了广泛应用。

话说，第一次看到这个裂缝临界长度计算公式时，Lg和结构尺度（比如上图c中的结构宽度）没有关系，我感觉很吃惊。我想，二者之间的关系大致隐藏在s里面，例如，结构宽度越小，s的提高速度越快，Lg也越小。

● 究竟会不会断裂？

关于裂缝，我是这么理解的。裂缝和变形一样，它们为结构使用者提供了一个观察结构是否安全，并及时做出反应的指标。如果结构在发生很小裂缝的情况下，人们还没来得及发现，结构就形成了自发性地破坏，这显然是很糟糕的。

这和我们说某个结构延性很差，是类似的概念。

根据常识，我们对裂缝的识别和结构的尺度有关，对船舶、桥梁、大型结构支撑等，裂缝发展到1~2m长，我们才能比较明显地观察到；而对一些小型构件，裂缝长度在1cm以内，我们就能观察到。

低碳钢的断裂功按10^5 J/m2计算，如果要容纳一条1m长的裂缝，则应力不能超过110Mpa；如果想要2m长的安全裂缝，则应力要减小到80Mpa；

对结构中的钢构件来说，正常工作应力一般不超过250Mpa，对应的允许裂缝长度约为20cm。

所以，格里菲斯的一个推论是，大体上，我们在小型结构中使用高强度金属和大工作应力要比在大型结构中更安全。结构越大，为安全起见，可承受的应力就越小。

大家是否想起了那句话：

如果我们的结构延性比较高，承载力就可以低一点；如果延性比较低，承载力就要高一些。

回到文章标题，应力集中（以及因此带来的小裂缝），为何没有导致结构断裂呢？大概是因为它们被结构延性给消化掉了吧。

本文参考资料：J.E.戈登 《结构是什么？》

来源：JIE 构生活（ID：gh_6e1c4b33c380），本文已获授权，对原作者表示感谢。

免责声明:本站部份内容由优秀作者和原创用户编辑投稿，本站仅提供存储服务，不拥有所有权,不承担法律责任。若涉嫌侵权/违法的，请与我联系，一经查实立刻删除内容。本文内容由快快网络小洁创作整理编辑！