钢结构稳定系数怎么求(钢结构稳定性怎么算)

导语：钢结构设计：线性稳定分析和计算长度系数

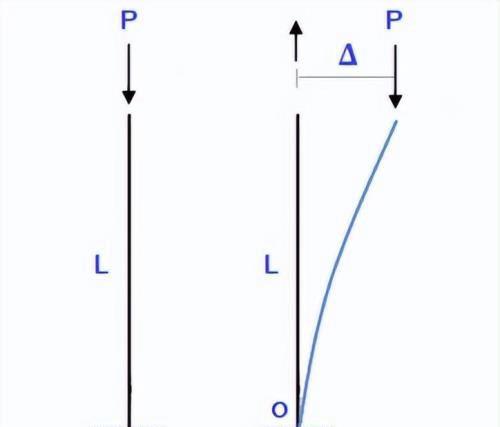
稳定是钢结构设计的重点，包括压杆稳定、受弯构件的问题、壳体的问题等。通过悬臂柱的稳定分析，试图说明稳定分析和线性分析的联系，减小对稳定的恐惧。

恐惧是因为不了解

将稳定分析和线性分析分开理解，很容易造成对稳定分析的恐惧。

将稳定全权交给软件来判断时，隔阂进一步加深了。

当看到讲稳定的教科书总是长篇累牍时，内心彻底绝望了。

失稳变形相比线性分析下的变形，固然大相径庭，但其理论基础是相同的，这就是平衡条件和变形协调条件，因此可以用线性分析的思维去理解稳定。

悬臂柱的计算长度系数估算

悬臂柱的稳定

假定侧向变形为抛物线：

为什么假定为抛物线？看起来像，正式的说法是满足约束边界条件。

支座弯矩（变形协调条件）：支座弯矩平衡条件：稳定承载力：

计算长度系数为2.22，理论解为2.0，相差11%。

计算长度系数的电算过程给定荷载分布下的静力分析特征值屈曲分析欧拉屈曲荷载Ncr = 屈曲系数φ x 静力分析下的轴力N

悬臂柱的计算长度系数电算描述

柱子长度2.5米，截面为P89x5（），材质钢（），柱顶压力1.2kN。

电算

特征值屈曲分析显示，第一阶屈曲模态对应的屈曲因子为79。

悬臂柱的特征值屈曲分析

计算长度系数：

小结

从悬臂柱的例子可以看出，稳定分析是建议在弯矩平衡条件之上的，弯矩则是由轴压力对侧向变形产生的（P-Δ效应），习惯上称之为附加弯矩，这就是稳定的本质。

线性分析因为忽略了附加弯矩而与稳定分析不同，当附加弯矩不可忽略时，需要进行稳定分析。

完备的理论、精度的解答是力学家的任务。工程师的任务是理解和应用这些成果，沿着力学家推导的过程走一遍，有时会陷入细节的泥潭，跳出来看有时更容易看到背后的本质。

这里讨论的稳定分析是小变形的稳定分析，以后讨论到非线性稳定时，将试图说明这些理解依然适用。

本文内容由小森整理编辑！