求线段值问题有多少种方法(如何求线段值问题)

导语：求线段和最值问题你觉得很难？不外乎就这12个基础图形，值得推荐

求线段和最值问题，最常见的一类考试题型，几乎每一场大考小考，都会出现。

那么，如何才能扎实的掌握这类题型呢？以下就是，12种求线段最值问题的基础图形，总结归纳，值得推荐。

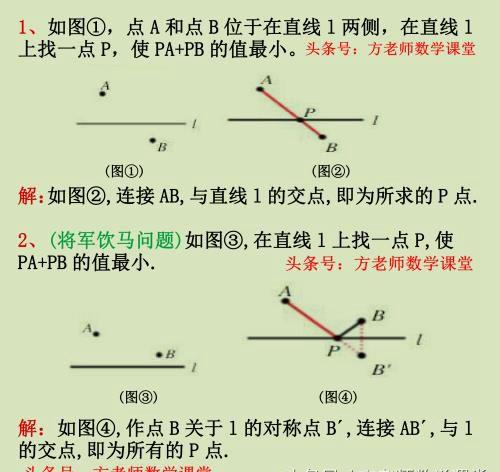
1、这是最简单的一种，A、B分别在直线的两侧，直接连接两点，两点之间线段最短。

2、将军饮马问题，因为对称性，PB=PB´，所以PA+PB=PA+PB´，转化成了第一种图形，两店之间线段最短。

3、因为对称性，PM=P´M，PN=P´´N，所以PM+MN+PN=P´M+MN+P´´N，两点之间线段最短，连接P´P´´就是最小值。

4、这个和第3个属于同一个道理。

5、经典造桥选址问题，因为MN的长度是固定不变的，只要找到AM+NB的最小值就好。平移点后，转化成了第一个图形。

6、因为CD的长度是固定不变的，只要找到AC+BD的最小值就好。平移线段AC，转成了第二个图形。

7、这个属于一定点，二动点求线段和最小值问题。根据对称性，PA+AB=P´A+AB，转化成了P´到直线l₂的距离，垂线段最短。

8、两线段差的绝对值要最小。谁的绝对值最小？当然是零的绝对值最小。

9、证明|PA-PB|的值最大？只要PA-PB的差最大就好。根据三角形的三边关系，两边之差小于第三边AB。当P、A、B三点共线的时候，PA-PB=AB，所以此刻差值最大。

10、原理一样，做对称，转化成第9个图。

11、两个定点，找两个动点，求线段和最小，就是做定点的反向对称点，再连接即可。

12、线段和最小值压轴难点，费马点。你会证明费马点这个结论吗？

练习题1、提示一下，属于第7个图的考题，结合勾股定理，三角形相似可得。

练习题2，同侧，两定点，求线段最小值，就是第2个图，将军饮马问题，没有难度。

3、第①小题简单，斜边上的中线等于斜边的一半。

第②小题，同侧两定点，求线段和最小值，将军饮马问题，作点D关于AC的对称点F，连接EF，求出即可。

练习题4，这个题看起来题目字数这么多，不要被吓倒，这题真的太简单。很多同学容易被字数多的题目吓倒。

仔细推敲，结合上面学的知识点，此题你要是不会做，我还不信了。

本文内容由小林整理编辑！